题目内容
一次函数y=ax+b(ab≠0)的图象不经过第二象限,则抛物线y=ax2+bx的顶点在
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
D
分析:根据一次函数y=ax+b(ab≠0)的图象不经过第二象限,则a>0,b<0,进而得出抛物线y=ax2+bx的顶点(- ,
,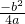 )所在象限.
)所在象限.
解答:∵一次函数y=ax+b(ab≠0)的图象不经过第二象限,
∴a>0,b<0,
∴抛物线y=ax2+bx的顶点(- ,
,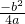 ),
),
- >0,
>0,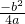 <0,
<0,
∴抛物线y=ax2+bx的顶点(- ,
,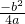 )在第四象限.
)在第四象限.
故选;D.
点评:此题主要考查了二次函数的性质以及一次函数的性质,根据已知得出a,b的符号是解题关键.
分析:根据一次函数y=ax+b(ab≠0)的图象不经过第二象限,则a>0,b<0,进而得出抛物线y=ax2+bx的顶点(-
 ,
,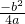 )所在象限.
)所在象限.解答:∵一次函数y=ax+b(ab≠0)的图象不经过第二象限,
∴a>0,b<0,
∴抛物线y=ax2+bx的顶点(-
 ,
,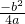 ),
),-
 >0,
>0,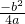 <0,
<0,∴抛物线y=ax2+bx的顶点(-
 ,
,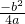 )在第四象限.
)在第四象限.故选;D.
点评:此题主要考查了二次函数的性质以及一次函数的性质,根据已知得出a,b的符号是解题关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
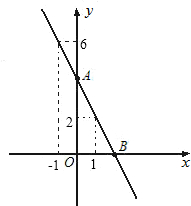 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: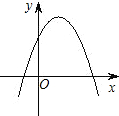 已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=
已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=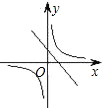
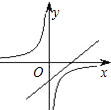
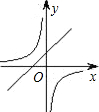
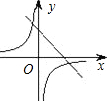
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=