题目内容
两个同心圆,小圆的切线被大圆截得的部分为6,则两圆围成的环形面积为________.
9π
分析:根据切线的性质定理、勾股定理以及垂径定理,得两圆半径之间的关系,故可求围成的环形面积=大圆面积-小圆面积.
解答: 解:如图:
解:如图:
∵AB=6,OC⊥AB,
∴AC=3,
∴圆环面积=π(OA2-OC2)=AC2=9π.
点评:注意:也可利用公式圆环的面积= 直接求出结果.(a是相切于小圆的大圆的弦).
直接求出结果.(a是相切于小圆的大圆的弦).
分析:根据切线的性质定理、勾股定理以及垂径定理,得两圆半径之间的关系,故可求围成的环形面积=大圆面积-小圆面积.
解答:
 解:如图:
解:如图:∵AB=6,OC⊥AB,
∴AC=3,
∴圆环面积=π(OA2-OC2)=AC2=9π.
点评:注意:也可利用公式圆环的面积=
 直接求出结果.(a是相切于小圆的大圆的弦).
直接求出结果.(a是相切于小圆的大圆的弦). 
练习册系列答案
相关题目
有两个同心圆,大圆的直径AB交小圆于C、D,大圆的弦EF切小圆于C点,ED交小圆于G点,若AO=6,CO=4,则EG等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
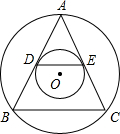 如图,两个同心圆,大圆的弦AB和AC分别切小圆于点D,E.求证:DE∥BC.
如图,两个同心圆,大圆的弦AB和AC分别切小圆于点D,E.求证:DE∥BC.