题目内容
⊙O的半径为12cm,弦AB为8cm,则圆心到AB的距离是 .
考点:垂径定理,勾股定理
专题:计算题
分析:作OC⊥AB于C,根据垂径定理得到AC=BC=
AB=4,然后在Rt△OAC中利用勾股定理计算OC即可.
| 1 |
| 2 |
解答:解:如图, 作OC⊥AB于C,则AC=BC=
作OC⊥AB于C,则AC=BC=
AB=4,
在Rt△OAC中,∵OA=12,AC=4,
OC=
=8
,
所以圆心到AB的距离为8
cm.
故答案为8
cm.
 作OC⊥AB于C,则AC=BC=
作OC⊥AB于C,则AC=BC=| 1 |
| 2 |
在Rt△OAC中,∵OA=12,AC=4,
OC=
| OA2-AC2 |
| 2 |
所以圆心到AB的距离为8
| 2 |
故答案为8
| 2 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.作弦的弦心距是常作的辅助线,可构造直角三角形,利用勾股定理计算.

练习册系列答案
相关题目
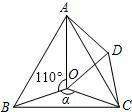 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.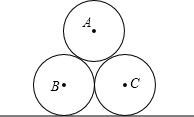 如图,某城市公园的雕塑是焊接固定在水平地面上的3个直径均为2m的两两外切的圆,请求出雕塑的最高点到地面的距离.(提示:构建适当的三角形辅助解答)
如图,某城市公园的雕塑是焊接固定在水平地面上的3个直径均为2m的两两外切的圆,请求出雕塑的最高点到地面的距离.(提示:构建适当的三角形辅助解答) 操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?
操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?