题目内容
在直角坐标系中,抛物线y=x2-2mx+n+1的顶点A在x轴负半轴上,与y轴交于点B,抛物线上一点C的横坐标为1,且AC=3 .
.(1)求此抛物线的函数解析式.
(2)若抛物线上有一点D,使得直线DB经过第一、二、四象限,且原点O到直线DB的距离为
 ,求这时点D的坐标.
,求这时点D的坐标.
【答案】分析:(1)先根据题意画出图形,过点C作CE⊥x轴于点E.由抛物线上一点C的横坐标为1,且AC=3 ,可用mn表示出C点坐标及OE,CE的长,由抛物线的顶点A在x轴负半轴上可得出A点坐标,再由方程有两个相等的实数根及勾股定理即可求出m、n的值,故可得出抛物线的解析式;
,可用mn表示出C点坐标及OE,CE的长,由抛物线的顶点A在x轴负半轴上可得出A点坐标,再由方程有两个相等的实数根及勾股定理即可求出m、n的值,故可得出抛物线的解析式;
(2)直线DB经过第一、二、四象限.设直线DB交x轴正半轴于点F,过点O作OM⊥OB于点M,由点O到直线DB的距离为 可得出OM的长,再根据抛物线y=x2+4x+4与y轴交于点B,可得出B点坐标,根据勾股定理求出BM的长,根据相似三角形的判定定理得出△OBF∽△MBO,根据相似三角形的对应边成比例可得出OF=2BO,故可得出F点的坐标,求出直线BF的解析式,再根据点D既在抛物线上,又在直线BF上可联立方程组,求出D点坐标.
可得出OM的长,再根据抛物线y=x2+4x+4与y轴交于点B,可得出B点坐标,根据勾股定理求出BM的长,根据相似三角形的判定定理得出△OBF∽△MBO,根据相似三角形的对应边成比例可得出OF=2BO,故可得出F点的坐标,求出直线BF的解析式,再根据点D既在抛物线上,又在直线BF上可联立方程组,求出D点坐标.
解答: 解:(1)根据题意画示意图(如图1),过点C作CE⊥x轴于点E.
解:(1)根据题意画示意图(如图1),过点C作CE⊥x轴于点E.
∵抛物线上一点C的横坐标为1,且AC=3 ,
,
∴C(1,n-2m+2),其中n-2m+2>0,
OE=1,CE=n-2m+2.
∵抛物线的顶点A在x轴负半轴上,
∴A(m,0),其中m<0,OA=-m,AE=OE+OA=1-m.
∴ ,
,
由①,得n=m2-1.③
把③代入②,整理得(m2-2m+1)2+(m2-2m+1)-90=0
(m2-2m+11)(m2-2m-8)=0.
∴m2-2m+11=0,或m2-2m-8=0.
∵△=(-2)2-4×11=-40<0,
∴方程m2-2m+11=0.没有实数根.
解方程m2-2m-8=0,得m1=4,m2=-2.
∵m<0,
∴m=-2.
把m=-2代入③,得n=3.
∴抛物线的函数解析式为y=x2+4x+4;
(2)解法一:∵直线DB经过第一、二、四象限.
∴设直线DB交x轴正半轴于点F,过点O作OM⊥OB于点M(如图2),
∵点O到直线DB的距离为 ,
,
∴OM=

∵抛物线y=x2+4x+4与y轴交于点B,
∴B(0,4)
∴OB=4.
∴BM= =
= =
= ,
,
∵OB⊥OF,OM⊥BF.
∴△OBF∽△MBO.
∴ =
= ,
,
∴ =
= ,
,
∴OF=2BO=8.
∴F(8,0).
∴直线BF的解析式为y=- x+4,
x+4,
∵点D既在抛物线上,又在直线BF上,
∴ ,解得
,解得 ,
, ,
,
∵DB是直线,
∴D与点B不重合.
∴D(- ,
, ),
),
解法二:过点D作DN⊥y轴于点N,设点D的横坐标为α.
同解法一,得OB=4,BM= ,
,
∵点D在抛物线y=x2+4x+4上,
∴D(α,α2+4α+4),且α<0,α2+4α+4>0.
∴DN=-α,ON=α2+4α+4,BN=ON-OB=α2+4α.
∵∠1=∠2,∠3=∠4=90°
∴△DNB∽△OMB,
∴ =
= ,
,
∴ =
= ,
,
整理得2α2+9α=0.解得α1=0,α2=- ,
,
∵DB是直线,
∴点D与点B不重合.
∴α=- ,此时α2+4α+4=
,此时α2+4α+4= ,
,
∴点D的坐标为(- ,
, ).
).
点评:本题考查的是二次函数综合题,涉及到勾股定理、相似三角形的判定与性质、用待定系数法求一次函数及二次函数的解析式等知识,难度适中.
 ,可用mn表示出C点坐标及OE,CE的长,由抛物线的顶点A在x轴负半轴上可得出A点坐标,再由方程有两个相等的实数根及勾股定理即可求出m、n的值,故可得出抛物线的解析式;
,可用mn表示出C点坐标及OE,CE的长,由抛物线的顶点A在x轴负半轴上可得出A点坐标,再由方程有两个相等的实数根及勾股定理即可求出m、n的值,故可得出抛物线的解析式;(2)直线DB经过第一、二、四象限.设直线DB交x轴正半轴于点F,过点O作OM⊥OB于点M,由点O到直线DB的距离为
 可得出OM的长,再根据抛物线y=x2+4x+4与y轴交于点B,可得出B点坐标,根据勾股定理求出BM的长,根据相似三角形的判定定理得出△OBF∽△MBO,根据相似三角形的对应边成比例可得出OF=2BO,故可得出F点的坐标,求出直线BF的解析式,再根据点D既在抛物线上,又在直线BF上可联立方程组,求出D点坐标.
可得出OM的长,再根据抛物线y=x2+4x+4与y轴交于点B,可得出B点坐标,根据勾股定理求出BM的长,根据相似三角形的判定定理得出△OBF∽△MBO,根据相似三角形的对应边成比例可得出OF=2BO,故可得出F点的坐标,求出直线BF的解析式,再根据点D既在抛物线上,又在直线BF上可联立方程组,求出D点坐标.解答:
 解:(1)根据题意画示意图(如图1),过点C作CE⊥x轴于点E.
解:(1)根据题意画示意图(如图1),过点C作CE⊥x轴于点E.∵抛物线上一点C的横坐标为1,且AC=3
 ,
,∴C(1,n-2m+2),其中n-2m+2>0,
OE=1,CE=n-2m+2.
∵抛物线的顶点A在x轴负半轴上,
∴A(m,0),其中m<0,OA=-m,AE=OE+OA=1-m.
∴
 ,
,由①,得n=m2-1.③
把③代入②,整理得(m2-2m+1)2+(m2-2m+1)-90=0
(m2-2m+11)(m2-2m-8)=0.
∴m2-2m+11=0,或m2-2m-8=0.
∵△=(-2)2-4×11=-40<0,
∴方程m2-2m+11=0.没有实数根.
解方程m2-2m-8=0,得m1=4,m2=-2.
∵m<0,
∴m=-2.
把m=-2代入③,得n=3.
∴抛物线的函数解析式为y=x2+4x+4;
(2)解法一:∵直线DB经过第一、二、四象限.
∴设直线DB交x轴正半轴于点F,过点O作OM⊥OB于点M(如图2),
∵点O到直线DB的距离为
 ,
,∴OM=


∵抛物线y=x2+4x+4与y轴交于点B,
∴B(0,4)
∴OB=4.
∴BM=
 =
= =
= ,
,∵OB⊥OF,OM⊥BF.
∴△OBF∽△MBO.
∴
 =
= ,
,∴
 =
= ,
,∴OF=2BO=8.
∴F(8,0).
∴直线BF的解析式为y=-
 x+4,
x+4,∵点D既在抛物线上,又在直线BF上,
∴
 ,解得
,解得 ,
, ,
,∵DB是直线,
∴D与点B不重合.
∴D(-
 ,
, ),
),解法二:过点D作DN⊥y轴于点N,设点D的横坐标为α.
同解法一,得OB=4,BM=
 ,
,∵点D在抛物线y=x2+4x+4上,
∴D(α,α2+4α+4),且α<0,α2+4α+4>0.
∴DN=-α,ON=α2+4α+4,BN=ON-OB=α2+4α.
∵∠1=∠2,∠3=∠4=90°
∴△DNB∽△OMB,
∴
 =
= ,
,∴
 =
= ,
,整理得2α2+9α=0.解得α1=0,α2=-
 ,
,∵DB是直线,
∴点D与点B不重合.
∴α=-
 ,此时α2+4α+4=
,此时α2+4α+4= ,
,∴点D的坐标为(-
 ,
, ).
).点评:本题考查的是二次函数综合题,涉及到勾股定理、相似三角形的判定与性质、用待定系数法求一次函数及二次函数的解析式等知识,难度适中.

练习册系列答案
相关题目
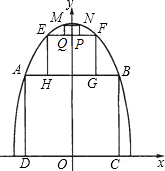 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: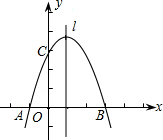 ,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
,B,C三点的抛物的对称轴为直线l,D为对称轴l上一动点.
 为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: (2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:
(2005•杭州)为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求: