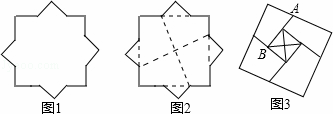
题目内容
如图1是由两块全等的含30°角的直角三角板摆放而成,斜边AC=10.
(1)若将△ADE沿直线AE翻折到如图2的位置,ED'与BC交于点F,求证:CF=EF;
(2)求EF的长;
(3)将图2中的△AD'E沿直线AE向右平移到图3的位置,使D'点落在BC上,求出平移的距离.

(1)证明:∵△ABC≌△ADE,
∴AC=AE,AB=AD,
根据翻折对称性,AD′=AD,
∴AD′=AB,
∴AC-AD′=AE-AB,
即CD′=BE,
在△CD′F与△EBF中,

∴△CD′F≌△EBF(AAS),
∴CF=EF(全等三角形对应边相等);
(2)解:∵∠C=30°,AC=10,
∴AB=AC=×10=5,
∴EB=10-AB=5,
在△EFB中,∠FEB=30°,
∴BF=EF,
根据勾股定理得EF2=BF2+EB2,
∴EF2=(EF)2+52,
解得EF= ;
;
(3)解:根据平移,D′D″∥AB,
又∵AD′=AB=5,CD′=10-AD′=5,
∴D′D″是△ABC的中位线,
∵∠C=30°,AC=10,
∴D′D″=AB=×AC=××10=,
故平移距离.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 ,恰好有三个整数解,则关于x的一次函数
,恰好有三个整数解,则关于x的一次函数 的图像与反比例函数
的图像与反比例函数 的图像的公共点的个数为 。
的图像的公共点的个数为 。 为:
为: ,有下列命题:
,有下列命题: ;
; 的根为:
的根为:
 的解集为
的解集为
 的图像与坐标轴交点组成的三角形面积为3,则此函数的顶点坐标是
的图像与坐标轴交点组成的三角形面积为3,则此函数的顶点坐标是 其中正确的( )
其中正确的( ) 和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.(原创)
和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.(原创)




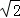 ,则图3中线段AB的长为 .
,则图3中线段AB的长为 .