题目内容
E，F分别为矩形ABCD的边AD，BC的中点，若矩形ABCD∽矩形EABF，AB=2，矩形ABCD的面积为
- A.
- B.
- C.4
- D.8
C
分析：根据相似多边形的对应边成比例，列式求出矩形ABCD的长，然后根据矩形的面积公式计算即可．
解答：∵E，F分别为矩形ABCD的边AD，BC的中点，
∴AE=
AD，
∵矩形ABCD∽矩形EABF，
∴
=
，
即AD2=AB2，
又∵AB=2，
解得AD=2，
∴矩形ABCD的面积=AB•AD=2×2=4．
故选C．
点评：本题主要考查了相似多边形的性质，利用相似多边形对应边成比例列出比例式是解题的关键．
分析：根据相似多边形的对应边成比例，列式求出矩形ABCD的长，然后根据矩形的面积公式计算即可．
解答：∵E，F分别为矩形ABCD的边AD，BC的中点，
∴AE=
AD，∵矩形ABCD∽矩形EABF，
∴
=，即
AD2=AB2，又∵AB=2，
解得AD=2
，∴矩形ABCD的面积=AB•AD=2×2
=4．故选C．
点评：本题主要考查了相似多边形的性质，利用相似多边形对应边成比例列出比例式是解题的关键．
练习册系列答案
相关题目
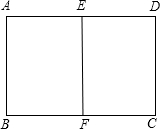如图，E，F分别为矩形ABCD的边AD，BC的中点，若矩形ABCD∽矩形EABF，AB=1．求矩形ABCD
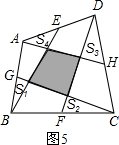
（2012•闵行区三模）已知：如图，在梯形ABCD中，AD∥BC，E、F分别为边AB、DC的中点，CG∥DE，交EF的延长线于点G．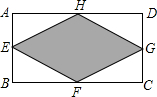
已知：如图，在矩形ABCD中，E，F，G，H分别为边AB，BC，CD，DA的中点．若AB=2，AD=4，则图中阴影部分的面积为
若从矩形一边上的点到对边的视角是直角，即称该点是直角点．例如，如图的矩形ABCD中，点M在CD边上，连接AM、BM，∠AMB=90°，则点M为直角点．若点M、N分别为矩形ABCD的边CD、AB上的直角点，且AB=4，BC=