题目内容
 (2012•玉林)如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3
(2012•玉林)如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3| 2 |
分析:延长A′B′交BC于点E,根据大正方形的对角线长求得其边长,然后求得小正方形的边长后即可求两个正方形的相似比.
解答: 解:∵在正方形ABCD中,AC=3
解:∵在正方形ABCD中,AC=3
∴BC=AB=3,
延长A′B′交BC于点E,
∵点A′的坐标为(1,2),
∴OE=1,EC=A′E=3-1=2,
∴OE:BC=1:3,
∴AA′:AC=1:3,
∵AA′=CC′,
∴AA′=CC′=A′C′,
∵O′A=O′C,
∴O′A:A′O′=3:1,
∴正方形A′B′C′D′与正方形ABCD的相似比是
.
故选B.
 解:∵在正方形ABCD中,AC=3
解:∵在正方形ABCD中,AC=3| 2 |
∴BC=AB=3,
延长A′B′交BC于点E,
∵点A′的坐标为(1,2),
∴OE=1,EC=A′E=3-1=2,
∴OE:BC=1:3,
∴AA′:AC=1:3,
∵AA′=CC′,
∴AA′=CC′=A′C′,
∵O′A=O′C,
∴O′A:A′O′=3:1,
∴正方形A′B′C′D′与正方形ABCD的相似比是
| 1 |
| 3 |
故选B.
点评:本题考查了位似变换和坐标与图形的变化的知识,解题的关键是根据已知条件求得两个正方形的边长.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
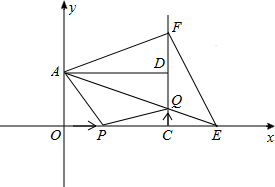 (2012•玉林)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2
(2012•玉林)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2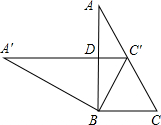 (2012•玉林)如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D=
(2012•玉林)如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D=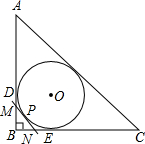 (2012•玉林)如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧
(2012•玉林)如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧
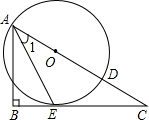 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 的双曲线y=
的双曲线y=