题目内容
在完全平方式a2+ab+k中,k=________.
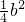
分析:完全平方公式:(a±b)2=a2±2ab+b2,这里首项是a的平方,根据完全平方公式即可求出.
解答:中间一项为ab=2a•
 b
b所以末项是
 b的平方
b的平方 b2,即k=
b2,即k= b2.
b2.故应填
 b2.
b2.点评:本题是完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.知道首项、中间项,求末项,从中间项2倍乘积中找到末项的平方根,就能求出末项的值.

练习册系列答案
相关题目
题目内容
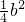
 b
b b的平方
b的平方 b2,即k=
b2,即k= b2.
b2. b2.
b2.