题目内容
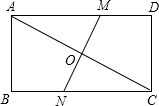矩形ABCD的边AB=4，AD=8，将这个矩形沿折痕MN对折，使两对角顶点中的A点恰好落在C点的位置，求AM的长．
分析：根据题中的翻折，可知∠AOM=∠COM=90°，可证出△AMO∽△ACD，
=
，根据AB=4，AD=8，可求出AO和AC的长，继而求出AM的长．
| AM |
| AC |
| AO |
| AD |
解答：解：由题意得：∠AOM=∠COM=90°，
又∠MAO=∠CAD，
∴△AMO∽△ACD，
∴
=
，
∵AB=4，AD=8，
∴AC=2AO=4
，
∴
=
，
解得：AM=5．
即AM的长为5．
又∠MAO=∠CAD，
∴△AMO∽△ACD，
∴
| AM |
| AC |
| AO |
| AD |
∵AB=4，AD=8，
∴AC=2AO=4
| 5 |
∴
| AM | ||
4
|
2
| ||
| 8 |
解得：AM=5．
即AM的长为5．
点评：本题考查翻折变换的知识，难度适中，注意掌握翻折是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
相关题目
如图，矩形ABCD的边AB=4，AD=10．点P是BC边上的一个点，如果△ABP与△CDP相似，那么符合条件的点P有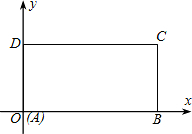
如图，在平面直角坐标系xoy中，已知矩形ABCD的边AB、AD分别在x轴、y轴上，点A与坐标原点重合，且AB=2，AD=1．
（2012•怀柔区二模）如图，矩形ABCD的边AB=5cm，BC=4cm动点P从A点出发，在折线AD-DC-CB上以1cm/s 的速度向B点作匀速运动，则表示△ABP的面积S（cm）与运动时间t（s）之间的函数系的图象是（ ）
如图，矩形ABCD的边AB在y轴上，AB的中点与原点重合，AB=2，AD=1，过定点Q（3，0）和动点P（0，a）的直线与矩形ABCD的边有公共点，则a的取值范围是（ ）