题目内容
如图,在△ACB中,∠ACB=90°,AC=4,BC=2,点P为射线CA上的一个动点,以P为圆心,1为半径作⊙P.(1)连接PB,若PA=PB,试判断⊙P与直线AB的位置关系,并说明理由;
(2)当PC为______

【答案】分析:(1)首先利用等腰三角形的性质得出AD=BD,再利用勾股定理得出AB的长,进而得出PD的长,即可得出⊙P与直线AB的位置关系;
(2)分别利用当⊙P与直线AB相切于点M,以及当⊙P′在线段CA的延长线上与直线AB相切于点N,利用相似三角形的性质得出PC的长即可,进而得出当⊙P与直线AB相交时,PC的取值范围;
(3)当△PMN为正三角形,即△PMN是边长为1的三角形,利用cos30°= ,求出PH的长,进而得出PA,PC的长,同理可得出当⊙P交在BA的延长线部分时,PC的长.
,求出PH的长,进而得出PA,PC的长,同理可得出当⊙P交在BA的延长线部分时,PC的长.
解答: 解:(1)如图1,过点P作PD⊥AB于点D,
解:(1)如图1,过点P作PD⊥AB于点D,
∵PA=PB,∴AD=BD,
在Rt△ACB中,AC=4,BC=2,
∴AB= ,∴AD=
,∴AD= ,
,
∵tan∠CAB= ,∴PD=
,∴PD= >1,
>1,
∴⊙P与直线AB相离;
(2)如图2,当⊙P与直线AB相切于点M,连接PM,
则PM⊥AB,
∵∠CAB=∠CAB,∠AMP=∠C=90°,
∴△APM∽△ABC,
∴ =
= ,
,
∵AB=2 ,
,
∴ =
= ,
,
解得:PC=4- ,
,
当⊙P′在线段CA的延长线上与直线AB相切于点N,连接PN,
则PN⊥AB,
∵∠NAP′=∠CAB,∠ANP′=∠C=90°,
∴△AP′N∽△ABC,
∴ =
= ,
,
∵AC=4,BC=2,
∴AB= =2
=2 ,
,
∴ =
= ,
,
解得:P′C=4+ ,
,
故当PC为4± 时,⊙P与直线AB相切,
时,⊙P与直线AB相切,
则当⊙P与直线AB相交时,写出PC的取值范围为 <PC<
<PC< ;
;
故答案为:4± ,
, <PC<
<PC< ;
; 
(3)如图3,当⊙P和线段AB相交时,过点P作PH⊥AB于点H,
∵△PMN为正三角形,即△PMN是边长为1的三角形;
∵cos30°= =
= ,
,
∴ ,
,
∵sin∠CAB= ,
,
∴PA= ,
,
∴PC=4- ;
;
当⊙P交在BA的延长线部分时,
过点P′作P′H′⊥AB于点H′,
∵△P′M′N′为正三角形,即△P′M′N′是边长为1的三角形;
∵cos30°= =
= ,
,
∴P′H′= ,
,
∵sin∠CAB=sin∠P′AH′= =
= ,
,
∴P′A= ,
,
P′C=4+ .
.
综上所述,PC=4- 或 PC=4+
或 PC=4+ .
.
点评:此题主要考查了圆的综合应用以及锐角三角函数的应用和相似三角形的判定与性质等知识,根据数形结合进行分类讨论得出是解题关键.
(2)分别利用当⊙P与直线AB相切于点M,以及当⊙P′在线段CA的延长线上与直线AB相切于点N,利用相似三角形的性质得出PC的长即可,进而得出当⊙P与直线AB相交时,PC的取值范围;
(3)当△PMN为正三角形,即△PMN是边长为1的三角形,利用cos30°=
 ,求出PH的长,进而得出PA,PC的长,同理可得出当⊙P交在BA的延长线部分时,PC的长.
,求出PH的长,进而得出PA,PC的长,同理可得出当⊙P交在BA的延长线部分时,PC的长.解答:
 解:(1)如图1,过点P作PD⊥AB于点D,
解:(1)如图1,过点P作PD⊥AB于点D,∵PA=PB,∴AD=BD,
在Rt△ACB中,AC=4,BC=2,
∴AB=
 ,∴AD=
,∴AD= ,
,∵tan∠CAB=
 ,∴PD=
,∴PD= >1,
>1,∴⊙P与直线AB相离;
(2)如图2,当⊙P与直线AB相切于点M,连接PM,
则PM⊥AB,
∵∠CAB=∠CAB,∠AMP=∠C=90°,

∴△APM∽△ABC,
∴
 =
= ,
,∵AB=2
 ,
,∴
 =
= ,
,解得:PC=4-
 ,
,当⊙P′在线段CA的延长线上与直线AB相切于点N,连接PN,
则PN⊥AB,
∵∠NAP′=∠CAB,∠ANP′=∠C=90°,
∴△AP′N∽△ABC,
∴
 =
= ,
,∵AC=4,BC=2,
∴AB=
 =2
=2 ,
,∴
 =
= ,
,解得:P′C=4+
 ,
,故当PC为4±
 时,⊙P与直线AB相切,
时,⊙P与直线AB相切,则当⊙P与直线AB相交时,写出PC的取值范围为
 <PC<
<PC< ;
;故答案为:4±
 ,
, <PC<
<PC< ;
; 
(3)如图3,当⊙P和线段AB相交时,过点P作PH⊥AB于点H,
∵△PMN为正三角形,即△PMN是边长为1的三角形;
∵cos30°=
 =
= ,
,∴
 ,
,∵sin∠CAB=
 ,
,∴PA=
 ,
,∴PC=4-
 ;
;当⊙P交在BA的延长线部分时,
过点P′作P′H′⊥AB于点H′,
∵△P′M′N′为正三角形,即△P′M′N′是边长为1的三角形;
∵cos30°=
 =
= ,
,∴P′H′=
 ,
,∵sin∠CAB=sin∠P′AH′=
 =
= ,
,∴P′A=
 ,
,P′C=4+
 .
.综上所述,PC=4-
 或 PC=4+
或 PC=4+ .
.点评:此题主要考查了圆的综合应用以及锐角三角函数的应用和相似三角形的判定与性质等知识,根据数形结合进行分类讨论得出是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 (2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=
(2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=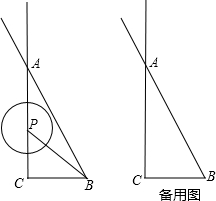 (2012•邯郸二模)如图,在△ACB中,∠ACB=90°,AC=4,BC=2,点P为射线CA上的一个动点,以P为圆心,1为半径作⊙P.
(2012•邯郸二模)如图,在△ACB中,∠ACB=90°,AC=4,BC=2,点P为射线CA上的一个动点,以P为圆心,1为半径作⊙P. 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标是
如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标是 如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F.
如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F. 如图,在△ACB中,点D是AB边上的一点,且∠ACB=∠CDA;点E在BC边上,且点E到AC、AB的距离相等,连接AE交CD于点F.试判断△CEF的形状;并证明你的结论.
如图,在△ACB中,点D是AB边上的一点,且∠ACB=∠CDA;点E在BC边上,且点E到AC、AB的距离相等,连接AE交CD于点F.试判断△CEF的形状;并证明你的结论.