题目内容
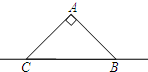 (2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=
(2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=2
或4
| 2 |
| 2 |
2
或4
.| 2 |
| 2 |
分析:应分△ACB向左平移或向右平移两种情况讨论,根据重合部分是等腰直角三角形,即可求得斜边的长,据此即可求解.
解答: 解:在△ACB中,∠CAB=90°,AC=AB=3,
解:在△ACB中,∠CAB=90°,AC=AB=3,
则BC=3
,
当△ABC沿直线BC平移,向左平移时:
△ACB与△A1C1B1重合部分是等腰直角三角形,
设直角边CD是a,则
a2=2,解得:a=2,
则CB1=2
.
当△ABC沿直线BC平移,向右平移时:
同理可得:C1B=2
,
则CC1=3
-2
=
,
则CB1=CC1+C1B1=
+3
=4
.
故CB1=2
或4
.
故答案是:2
或4
.
 解:在△ACB中,∠CAB=90°,AC=AB=3,
解:在△ACB中,∠CAB=90°,AC=AB=3,则BC=3
| 2 |
当△ABC沿直线BC平移,向左平移时:
△ACB与△A1C1B1重合部分是等腰直角三角形,
设直角边CD是a,则
| 1 |
| 2 |
则CB1=2
| 2 |
当△ABC沿直线BC平移,向右平移时:

同理可得:C1B=2
| 2 |
则CC1=3
| 2 |
| 2 |
| 2 |
则CB1=CC1+C1B1=
| 2 |
| 2 |
| 2 |
故CB1=2
| 2 |
| 2 |
故答案是:2
| 2 |
| 2 |
点评:本题考查了图形的平移,注意到重合部分是等腰直角三角形,以及两种情况进行讨论是关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
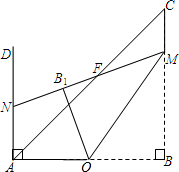 (2012•虹口区二模)如图,△ABC中,∠ABC=90°,AB=BC=4,点O为AB边的中点,点M是BC边上一动点(不与点B、C重合),AD⊥AB,垂足为点A.连接MO,将△BOM沿直线MO翻折,点B落在点B1处,直线M B1与AC、AD分别交于点F、N.
(2012•虹口区二模)如图,△ABC中,∠ABC=90°,AB=BC=4,点O为AB边的中点,点M是BC边上一动点(不与点B、C重合),AD⊥AB,垂足为点A.连接MO,将△BOM沿直线MO翻折,点B落在点B1处,直线M B1与AC、AD分别交于点F、N.