Question

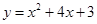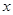如图，已知抛物线交轴于A、B两点，交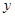轴于点C，抛物线的对称轴交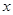轴于点E，点B的坐标为（，0）．

【小题1】求抛物线的对称轴及点A的坐标
【小题2】在平面直角坐标系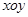中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由；
【小题3】连结CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的解析式；若不存在，请说明理由．

Answer 1

p;【答案】
【小题1】① 对称轴
② 当时，有
解之，得，
∴ 点A的坐标为（，0）
【小题2】满足条件的点P有3个，分别为（，3），（2，3），（，）．）
【小题3】存在．）
当时，   ∴ 点C的坐标为（0，3）
∵ DE∥轴，AO3，EO2，AE1，CO3
∴ ∽  ∴     即  ∴ DE1
∴ 4
在OE上找点F，使OF，此时2，直线CF把四边形DEOC
分成面积相等的两部分，交抛物线于点M．
设直线CM的解析式为，它经过点．
则 
解之，得    ∴ 直线CM的解析式为解析:
p;【解析】略