题目内容
 如图,已知点A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC=
如图,已知点A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC=| 1 | 2 |
分析:根据已知若能证明∠OAB=90°,则AB是⊙O的切线,否则不是.根据题意可知OA=OC=AC=
OB,可得△OAC是等边三角形与△ABC是等腰三角形,则可求得角的度数,得解.
| 1 |
| 2 |
解答:解:∵OC=BC,AC=
OB,
∴AC=OA=OC,
∴∠OAC=60°;
∴∠OCA=2∠CBA=60°,
∴∠CAB=30°,
∴∠OAB=60°+30°=90°;
∴AB是⊙O的切线.
| 1 |
| 2 |
∴AC=OA=OC,
∴∠OAC=60°;
∴∠OCA=2∠CBA=60°,
∴∠CAB=30°,
∴∠OAB=60°+30°=90°;
∴AB是⊙O的切线.
点评:本题考查了切线的判定与特殊三角形的性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
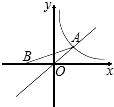 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=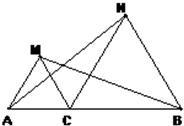 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.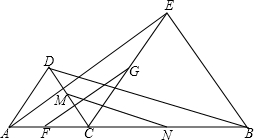 M、N分别是线段AC、CE、CD、CB的中点,
M、N分别是线段AC、CE、CD、CB的中点,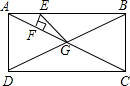 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG= 如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.
如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.