Question

【题目】在学习了数轴后，小亮决定对数轴进行变化应用：

（1）应用一：已知点在数轴上表示为-2，数轴上任意一点表示的数为，则两点的距离可以表示为 ；应用这个知识，请写出当 时， 有最小值为 ．

（2）应用二：从数轴上取下一个单位长度的线段，第一次剪掉原长的，第二次剪掉剩下的，依此类推，每次都剪掉剩下的，则剪掉4次后剩下线段长度为 ；应用这个原理，请计算：；

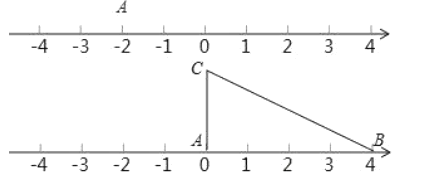
（3）应用三：如图，将一根拉直的细线看作数轴，一个三边长分别为，，的三角形的顶点与原点重合，边在数轴正半轴上，将数轴正半轴的线沿的顺序依次缠绕在三角形的边上，负半轴的线沿的顺序依次缠绕在三角形的边上．

①如果正半轴的线缠绕了3圈，负半轴的线缠绕了5圈，求绕在点上的所有数之和；

②如果正半轴的线不变，将负半轴的线拉长一倍，即原线上的点-2的位置对应着拉长后的数-1，并将三角形向正半轴平移一个单位后再开始绕，求绕在点且绝对值不超过60的所有数之和．

Answer 1

【答案】（1），，14；（2），；（3）①；②-160

【解析】

(1)根据数轴上两点间的距离的表示来列式即可；

(2)第一次剪掉的长度是，剩下的长度是；第二次剪掉的长度是，剩下的长度是；以此类推，即可求得答案；

(3)①分别找出正半轴和负半轴在点C上的数字之间的规律，即可求出所有数字之和；

②分别找出绕在点B且绝对值不超过60的所有数字，求和即可．

(1)已知点A在数轴上表示为，数轴上任意一点B表示的数为，则AB两点的距离可以表示为；

根据的几何意义，可得：

表示到数轴上，3，0，5，6五个数的距离之和，

∴当与重合时，有最小值，最小值为14，此时．

故答案为：，，14；

(2)第一次剪掉的长度是，剩下的长度是；

第二次剪掉的长度是，剩下的长度是；

第三次剪掉的长度是，剩下的长度是；

第四次剪掉的长度是，剩下的长度是；

，

第八次剪掉的长度是，剩下的长度是；

∴，

故答案为：，；

(3)①如果正半轴的线缠绕了5圈，绕在点C的数字分别为：9，21，33，45，57；
负半轴的线缠绕了3圈，绕在点C的数字分别为：-3，-15，-27．
则绕在点C上的所有数字之和为：；

②如果正半轴的线不变，并将三角形ABC向正半轴平移一个单位后再开始绕，
则正半轴上绕在点B且绝对值不超过60的数字有：5，17，29，41，53；
将负半轴的线拉长一倍，并将三角形ABC向正半轴平移一个单位后再开始绕，
则负半轴上绕在点B且绝对值不超过60的数字有：-3.5，-9.5，-15.5，-21.5，-27.5，-33.5，-39.5，-45.5，-51.5，-57.5．
则绕在点B且绝对值不超过60的数字之和为：．

故答案为：①；②．