题目内容
【题目】已知在
中，
，
分别为
边上的两动点，且在运动过程中保持
，
为的对角线．
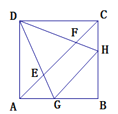
（1）如图①，若
，
图①
①当点
与点
重合时，探索
的值；
②当点与点不重合时，探索的值；
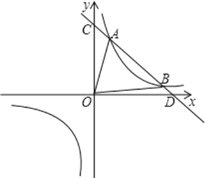
（2）如图②，参考（1）研究方法，若
，
图②
①当点与点重合时，探索
的值；
②当点与点不重合时，探索的值；
（3）如图③，参考（1）（2）研究方法，若
时，试探索是否存在常数
，使得
，若存在，请直接写出的值，若不存在，请说明理由．
【答案】（1）①
；②；
（2）①
；②；
（3）
．
【解析】
（1）①利用等边三角形的性质即可解决问题；
②如图①中，只要证明
即可解决问题；
（2）①解直角三角形求出有关线段即可解决问题；②若点
与点
不重合，如图②中，过点
作
于点
，设
，
，只要证明
，可得
，在
中，
，可得
，
，推出
，在
中，由
，可得
，由此即可解决问题；
（3）模仿（1）（2）的解法即可解决问题；
解；（1）①如图①﹣1中，
图①-1
四边形
是平行四边形，
，
都是等边三角形
点与点重合
点
与点
重合
，
．
②若点与点不重合．如图①中，
图①
由①得
，都是等边三角形
，
（2）①若点与点重合，如图②﹣1中，
图②-1
，
易知
，又
，
又
容易证得
设
，则
，
，
又
，
．
若点与点不重合，如图②中，过点作于点，
设，
图②
由上可知
，
，
，
，又
，
，
，
在中，
，
，，
，
在中，
，
，
，
，
，
（3）如图③当点与重合时，作
于
，
于．
设
，
．
图③
则
，
，
，
，
，
，
由
，可得
，
，
，
，
，
．
由（1）（2）可知：当点与点不重合时，
，
综上所述，．
练习册系列答案
相关题目
【题目】某校选拔射击运动员参加比赛，甲、乙两人在相同的条件下连续射靶各
次，命中的环数（均为不大于10的正整数）如表：
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
（1）当
为何值时，选派乙去参加比赛更合适，请说明理由；
（2）若乙最后两次射靶均命中
环，则选派谁去参加比赛更合适？请说明理由．
