题目内容
先阅读材料,再根据材料中所提供的方法解答下列问题:
我们在求1+2+3+…+99+100的值时,可以用下面的方法:
我们设S=1+2+3+…+99+100①,那么S=100+99+98+…+3+2+1②.
然后,我们由①+②,得2S=(100+1)+(99+2)+(98+3)+…+(99+2)+(100+1),共100个101.
2S=101+101+101+…+101=100×101,
所以S=100×101÷2=5050.
依据上述方法,求下列各式的值:
(1)1+3+5+…+97+99;
(2)5+10+15+…+195+200.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某天早上,一辆巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,若规定向东行驶为正,向西行驶为负,行驶记录如下表(单位:千米),则巡逻车在巡逻过程中,与A地的最远距离是( )
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
+10 | -2 | +5 | +12 | -3 | +2 | -10 |
A. 44千米 B. 36千米 C. 25千米 D. 14千米




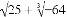 +(﹣1)2017;
+(﹣1)2017; 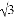 ﹣2|+2(
﹣2|+2(