题目内容
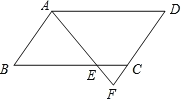
【题目】已知，将矩形ABCD折叠，使点C与点A重合，点D落在点G处，折痕为EF．
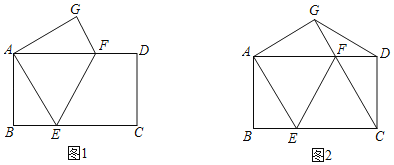
（1）如图1，求证：BE＝GF；
（2）如图2，连接CF、DG，若CE＝2BE，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形，使写出的每个三角形都为等腰三角形
【答案】（1）见解析；（2）△CEF，△AGD，△FGD，△DGC，△AEF是等腰三角形．
【解析】
（1）根据题意，通过证明
即可得到
；
（2）根据题意将矩形ABCD折叠，使点C与点A重合，点D落在点G处，通过等腰三角形的判定及性质即可得到
是等腰三角形.
（1）证明∵矩形ABCD
∴
由折叠可知：
∴
∴
，且
∴
∴；
（2）证明：∵将矩形ABCD折叠，使点C与点A重合，点D落在点G处
∴
∴
是等腰三角形
∵
∴
∴
∴
∴
是等腰三角形
∵
∴
，且
∴
∴
∵
∴
∴
∴
∴
∴
∴
是等腰三角形
综上所述：是等腰三角形．
阅读快车系列答案【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征，其中流量
（辆
小时）指单位时间内通过道路指定断面的车辆数；速度
（千米小时）指通过道路指定断面的车辆速度，密度
（辆千米）指通过道路指定断面单位长度内的车辆数．为配合大数据治堵行动，测得某路段流量与速度之间关系的部分数据如下表：
速度v（千米/小时） |
|
|
|
|
|
|
|
|
流量q（辆/小时） |
|
|
|
|
|
|
|
|
（1）根据上表信息，下列三个函数关系式中，刻画，关系最准确是_____________________．（只填上正确答案的序号）
①
；②
；③
（2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？
（3）已知，，满足
，请结合（1）中选取的函数关系式继续解决下列问题：市交通运行监控平台显示，当
时道路出现轻度拥堵．试分析当车流密度在什么范围时，该路段将出现轻度拥堵？
【题目】某班共30名同学参加了网络上第二课堂的禁毒知识竞赛（共20道选择题），学习委员对竞赛结果进行了统计，发现每个人答题正确题数都超过15题．通过统计制成了下表，结合表中信息，解答下列问题：
答对题数 | 16 | 17 | 18 | 19 | 20 |
人数 | 3 | 9 | 6 | 4 |
（1）补统计表中数据：
（2）求这30名同学答对题目的平均数、众数和中位数；
（3）答题正确率为100%的4名同学中恰好是2名男同学和2名女同学，现从中随机抽取2名同学参加学校禁毒知识抢答大赛，问抽到1男1女的概率是多少？
【题目】一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：
会员年卡类型 | 办卡费用（元） | 每次游泳收费（元） |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如，购买A类会员年卡，一年内游泳20次，消费50+25×20＝550元，若一年内在该游泳馆游泳的次数介于40～50次之间，则最省钱的方式为（ ）
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
