题目内容
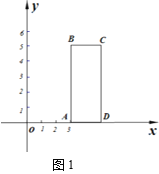
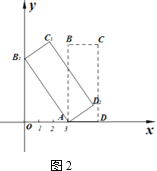
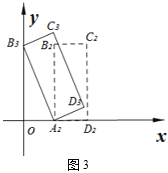
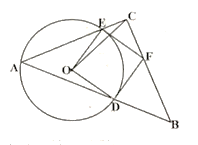
【题目】如图,等腰![]() 的一个锐角顶点
的一个锐角顶点![]() 是
是![]() 上的一个动点,
上的一个动点,![]() ,腰
,腰![]() 与斜边
与斜边![]() 分别交
分别交![]() 于点
于点![]() ,分别过点
,分别过点![]() 作
作![]() 的切线交于点
的切线交于点![]() ,且点
,且点![]() 恰好是腰
恰好是腰![]() 上的点,连接
上的点,连接![]() ,若
,若![]() 的半径为4,则
的半径为4,则![]() 的最大值为:( )
的最大值为:( )
A.![]() B.
B.![]() C.6D.8
C.6D.8
【答案】A
【解析】
先由等腰三角形的性质、切线的性质及圆的半径相等判定四边形ODFE是正方形,再得出点C在以EF为直径的半圆上运动,则当OC经过半圆圆心G时,OC的值最大,用勾股定理计算出OG的长度,再加上CG的长度即可.
解:∵等腰Rt△ABC中,∠ACB=90°,
∴∠A=∠B=45°,
∴∠DOE=2∠A=90°,
∵分别过点D,E作⊙O的切线,
∴OD⊥DF,OE⊥EF,
∴四边形ODFE是矩形,
∵OD=OE=4,
∴四边形ODFE是正方形,
∴EF=4,
∵点F恰好是腰BC上的点,
∴∠ECF=90°
∴点C在以EF为直径的半圆上运动,
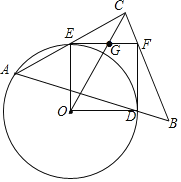
∴设EF的中点为G,则EG=FG=CG=![]() EF=2,且当OC经过半圆圆心G时,OC的值最大,此时,在Rt△OEG中,OG=
EF=2,且当OC经过半圆圆心G时,OC的值最大,此时,在Rt△OEG中,OG=![]() ,
,
∴OC=OG+CG=![]() .
.
故答案为:A.

【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() .
.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
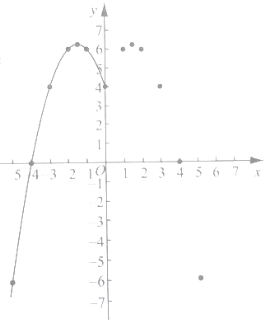
(3)观察函数图象,写出两条函数的性质.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有
有![]() 个不相等的实数根,则
个不相等的实数根,则![]() 的取值范围为 .
的取值范围为 .