题目内容
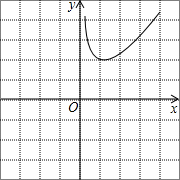 阅读下列材料,回答问题.
阅读下列材料,回答问题.材料一:人们习惯把形如y=x+
| k |
| x |
材料二:对任意的实数a、b而言,a2-2ab+b2=(a-b)2≥0,即a2+b2≥2ab.
易知当a=b时,(a-b)2=0,即:a2-2ab+b2=0,所以a2+b2=2ab.
若a≠b,则(a-b)2>0,所以a2+b2>2ab.
材料三:如果一个数的平方等于m,那么这个数叫做m的平方根(square root).一个正数有两个平方根,它们互为相反数.0的平方根是0,负数没有平方根.
问题:
(1)若“根号函数”y=x+
| 1 |
| x |
(2)请根据材料二、三给出的信息,试说明:当x>0时,函数y=x+
| 1 |
| x |
分析:(1)根据材料一,函数的图象关于原点中心对称,可得函数图象;
(2)将y=x+
化为y=
=
,再根据材料二、三所给条件解答.
(2)将y=x+
| 1 |
| x |
(x+
|
x2+
|
解答:解:(1)根据材料一,函数的图象关于原点中心对称,可得函数图象:
(2)∵x>0,
∴y=
=
,
又∵x2+
-2x•
=(x-
)2≥0,
∴x2+
≥2,
∴y=
=
≥
=2,
即y≥2,
∴函数y=x+
的最小值为2.

(2)∵x>0,
∴y=
(x+
|
x2+
|
又∵x2+
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
∴x2+
| 1 |
| x2 |
∴y=
(x+
|
x2+
|
| 2+2 |
即y≥2,
∴函数y=x+
| 1 |
| x |
点评:本题考查了反比例函数综合题,读懂材料并加以运用是解题的关键.

练习册系列答案
相关题目
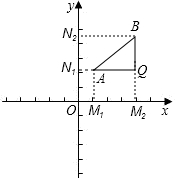 原点,半径为r的圆的方程.
原点,半径为r的圆的方程.