题目内容
如图，一把角尺的一边和一条钢管的轴截面⊙O相切于点A，另一端点B在⊙O上，角尺的直角顶点为C，已知AC=8，BC=6，那么⊙O的直径长是分析：延长CB交圆于点E，作OF⊥CE于点F，连接OA．根据切割线定理、垂径定理、勾股定理先求半径，然后得解．
解答：
解：如图，延长CB交圆于点E，作OF⊥CE于点F，连接OA．
则四边形OACF是矩形，有OF=CA．
由切割线定理知，AC2=BC•CE，解得CE=
，
BE=CE-BC=
．
由垂径定理知，BF=
BE=
．
由勾股定理得，OB=
，
所以圆的直径=
．
解：如图，延长CB交圆于点E，作OF⊥CE于点F，连接OA．则四边形OACF是矩形，有OF=CA．
由切割线定理知，AC2=BC•CE，解得CE=
| 32 |
| 3 |
BE=CE-BC=
| 14 |
| 3 |
由垂径定理知，BF=
| 1 |
| 2 |
| 7 |
| 3 |
由勾股定理得，OB=
| 25 |
| 3 |
所以圆的直径=
| 50 |
| 3 |
点评：本题利用了切线的性质，切割线定理，垂径定理，勾股定理，矩形的性质求解．建模思想是解决本题的关键．
练习册系列答案
相关题目
尺放在给出的图形上，使直角顶点P在线段EF（包括端点）上滑动，直角的一边始终经过点C，另一边与BF相交于G，连接AP．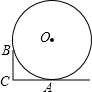
如图，一把角尺的一边和一条钢管的轴截面⊙O相切于点A，另一端点B在⊙O上，角尺的直角顶点为C，已知AC=8，BC=6，那么⊙O的直径长是________．