题目内容
如图，∠BOA=30°，P为角平分线上一点，DP⊥OA垂足为D，PC∥OA，交OB于C，若PC=10cm，则DP的长为________cm．
5
分析：过点P作PE⊥OB于E，根据两直线平行，同位角相等可得∠PCE=∠BOA，再根据直角三角形30°角所对的直角边等于斜边的一半求出PE，然后根据角平分线上的点到角的两边的距离相等解答．
解答：
解：如图，过点P作PE⊥OB于E，
∵PC∥OA，∠BOA=30°，
∴∠PCE=∠BOA=30°，
∴PE=
PC=×10=5cm，
∵OP是∠BOA的平分线，
∴DP=PE=5cm．
故答案为：5．
点评：本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，角平分线上的点到角的两边的距离相等的性质，平行线的性质，熟记性质并作出辅助线是解题的关键．
分析：过点P作PE⊥OB于E，根据两直线平行，同位角相等可得∠PCE=∠BOA，再根据直角三角形30°角所对的直角边等于斜边的一半求出PE，然后根据角平分线上的点到角的两边的距离相等解答．
解答：
解：如图，过点P作PE⊥OB于E，∵PC∥OA，∠BOA=30°，
∴∠PCE=∠BOA=30°，
∴PE=
PC=×10=5cm，∵OP是∠BOA的平分线，
∴DP=PE=5cm．
故答案为：5．
点评：本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，角平分线上的点到角的两边的距离相等的性质，平行线的性质，熟记性质并作出辅助线是解题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
（2013•六盘水）已知．在Rt△OAB中，∠OAB=90°，∠BOA=30°，OA=
如图，∠BOA是平角，∠BOD=∠AOD，∠1=∠4=30°，则互为余角的共有
如图，∠BOA=30°，P为角平分线上一点，DP⊥OA垂足为D，PC∥OA，交OB于C，若PC=10cm，则DP的长为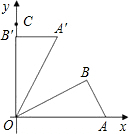
（创新学习）如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．