题目内容
 已知:如图,平面直角坐标系中,点A、B的坐标分别是A(1,4);B(3,0),以AB为直径的圆M与y轴相交于点C、D(点C在D的下方).
已知:如图,平面直角坐标系中,点A、B的坐标分别是A(1,4);B(3,0),以AB为直径的圆M与y轴相交于点C、D(点C在D的下方).(1)求直线AB的函数解析式和线段AB的长;
(2)判断△ABC的形状,并说明理由;
(3)若点P在以AB为直径的圆M上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,求点Q的坐标.
分析:(1)利用待定系数法确定直线AB的解析式;运用两点的距离公式可计算得到AB=2
;
(2)由于AB为⊙M的直径,根据圆周角定理得∠ACB=90°,设C点坐标为(0,t),根据两点的距离公式得到BC2=(3-0)2+(0-t)2,AC2=1+(4-t)2,
然后利用勾股定理得9+t2+1+(4-t)2=20,解得t1=1,t2=3,则C点坐标为(0,1),所以BC2=9+t2=10,AC2=1+(4-t)2=10,即AC=BC,于是可判断△ABC为等腰直角三角形;
(3)设P点坐标为(a,b),先证明Rt△APB∽Rt△BOC,利用
=
=
可计算出PA=3
,PB=
,再根据两点的距离公式得到(a-1)2+(b-4)2=(3
)2,(a-3)2+(b-0)2=(
)2,可解得a=
,b=-
;a=4,b=1;然后利用待定系数法确定直线AP的解析式,最后确定Q点坐标.
| 5 |
(2)由于AB为⊙M的直径,根据圆周角定理得∠ACB=90°,设C点坐标为(0,t),根据两点的距离公式得到BC2=(3-0)2+(0-t)2,AC2=1+(4-t)2,
然后利用勾股定理得9+t2+1+(4-t)2=20,解得t1=1,t2=3,则C点坐标为(0,1),所以BC2=9+t2=10,AC2=1+(4-t)2=10,即AC=BC,于是可判断△ABC为等腰直角三角形;
(3)设P点坐标为(a,b),先证明Rt△APB∽Rt△BOC,利用
| PA |
| OB |
| BP |
| OC |
| AB |
| BC |
| 2 |
| 2 |
| 2 |
| 2 |
| 7 |
| 5 |
| 1 |
| 5 |
解答:解:(1)设直线AB的解析式为y=kx+b(k≠0),
把A(1,4);B(3,0)代入得
,
解得
,
所以直线AB的解析式为y=-2x+6;
线段AB的长=
=2
;
(2)△ABC为等腰直角三角形.理由如下:
∵AB为⊙M的直径,
∴∠ACB=90°,
∴AC2+BC2=AB2,
设C点坐标为(0,t),
∴BC2=(3-0)2+(0-t)2=9+t2,AC2=(1-0)2+(4-t)2=1+(4-t)2,
而AB=2
,
∴9+t2+1+(4-t)2=20,
解得t1=1,t2=3,
∴C点坐标为(0,1),
∴BC2=9+t2=10,AC2=1+(4-t)2=10,即AC=BC,
∴△ABC为等腰直角三角形;
(3)如图,∵AB为⊙M的直径,
∴∠APB=90°,
∵∠BAP=∠OBC,
∴Rt△APB∽Rt△BOC,
∴
=
=
,即
=
=
=
,
∴PA=3
,PB=
,
设P点坐标为(a,b),
∴(a-1)2+(b-4)2=(3
)2,(a-3)2+(b-0)2=(
)2,
∴a=
,b=-
;a=4,b=1;
∴P点坐标为(
,-
)或(4,1),
设直线AP的解析式为y=mx+n,
过A(1,4)和P(
,-
)的解析式为y=-7x+11,把y=0代入得-7x+11=0,解得x=
,则Q点坐标为(
,0);
过A(1,4)和P(4,1)的解析式为y=-x+5,把y=0代入得-x+5=0,解得x=5,则Q点坐标为(5,0);
∴满足条件的Q点坐标为(
,0)或(5,0).

把A(1,4);B(3,0)代入得
|
解得
|
所以直线AB的解析式为y=-2x+6;
线段AB的长=
| (1-3)2+(4-0)2 |
| 5 |
(2)△ABC为等腰直角三角形.理由如下:
∵AB为⊙M的直径,
∴∠ACB=90°,
∴AC2+BC2=AB2,
设C点坐标为(0,t),
∴BC2=(3-0)2+(0-t)2=9+t2,AC2=(1-0)2+(4-t)2=1+(4-t)2,
而AB=2
| 5 |
∴9+t2+1+(4-t)2=20,
解得t1=1,t2=3,
∴C点坐标为(0,1),
∴BC2=9+t2=10,AC2=1+(4-t)2=10,即AC=BC,
∴△ABC为等腰直角三角形;
(3)如图,∵AB为⊙M的直径,
∴∠APB=90°,
∵∠BAP=∠OBC,
∴Rt△APB∽Rt△BOC,
∴
| PA |
| OB |
| BP |
| OC |
| AB |
| BC |
| PA |
| 3 |
| BP |
| 1 |
2
| ||
|
| 2 |
∴PA=3
| 2 |
| 2 |
设P点坐标为(a,b),
∴(a-1)2+(b-4)2=(3
| 2 |
| 2 |
∴a=
| 8 |
| 5 |
| 1 |
| 5 |
∴P点坐标为(
| 8 |
| 5 |
| 1 |
| 5 |
设直线AP的解析式为y=mx+n,
过A(1,4)和P(
| 8 |
| 5 |
| 1 |
| 5 |
| 11 |
| 7 |
| 11 |
| 7 |
过A(1,4)和P(4,1)的解析式为y=-x+5,把y=0代入得-x+5=0,解得x=5,则Q点坐标为(5,0);
∴满足条件的Q点坐标为(
| 11 |
| 7 |
点评:本题考查了圆的综合题:熟练掌握圆周角定理和待定系数法求函数的解析式;记住两点的距离公式;会运用勾股定理和三角形相似比进行几何计算.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
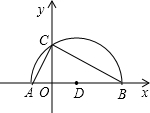 BC=4
BC=4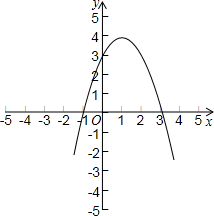 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3). 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.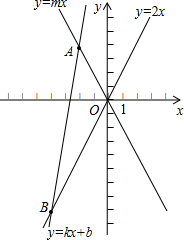 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).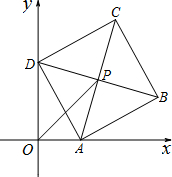 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.