题目内容
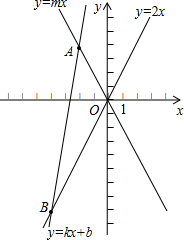 已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:如图,平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).(1)求直线y=mx(m≠0)的解析式;
(2)若直线y=kx+b(k≠0)与另一条直线y=2x交于点B,且点B的横坐标为-4,求△ABO的面积.
分析:(1)把点A(-2,4)代入直线y=mx,运用待定系数法即可求出直线y=mx(m≠0)的解析式;
(2)先把x=-4代入y=2x,求出点B的坐标,再将A、B两点的坐标代入y=kx+b,运用待定系数法求出其解析式,设直线AB与x轴交于点C,则△ABO的面积=△AOC的面积+△BOC的面积.
(2)先把x=-4代入y=2x,求出点B的坐标,再将A、B两点的坐标代入y=kx+b,运用待定系数法求出其解析式,设直线AB与x轴交于点C,则△ABO的面积=△AOC的面积+△BOC的面积.
解答:解:(1)∵点A(-2,4)在直线y=mx上,
∴4=-2m,
∴m=-2.
∴y=-2x;
 (2)设直线AB与x轴交于点C.
(2)设直线AB与x轴交于点C.
把x=-4代入y=2x,得y=-8,
∴点B的坐标为(-4,-8).
∵点A(-2,4)、点B(-4,-8)在直线y=kx+b上,
∴
,
解得
,
∴y=6x+16.
令y=0,得x=-
.
∴点C的坐标为(-
,0),
∴△ABO的面积=△AOC的面积+△BOC的面积=
×
×4+
×
×8=16.
∴4=-2m,
∴m=-2.
∴y=-2x;
 (2)设直线AB与x轴交于点C.
(2)设直线AB与x轴交于点C.把x=-4代入y=2x,得y=-8,
∴点B的坐标为(-4,-8).
∵点A(-2,4)、点B(-4,-8)在直线y=kx+b上,
∴
|
解得
|
∴y=6x+16.
令y=0,得x=-
| 8 |
| 3 |
∴点C的坐标为(-
| 8 |
| 3 |
∴△ABO的面积=△AOC的面积+△BOC的面积=
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
点评:本题考查了运用待定系数法求一次函数的解析式,交点坐标的求法及三角形的面积,属于基础题型,难度中等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 BC=4
BC=4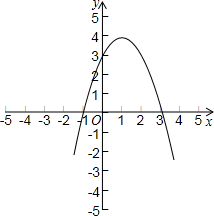 、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3).
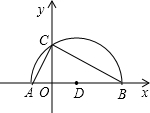
、B,其中点B在点A的右侧,抛物线图象与y轴交于点C,且经过点D(2,3). 已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.
已知:如图在平面直角坐标系xOy中,直线AB分别与x,y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OA=3,OB=6,OE=2.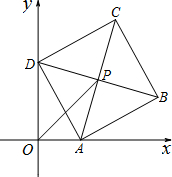 已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.
已知:如图,平面直角坐标系xOy中,正方形ABCD的边长为4,它的顶点A在x轴的正半轴上运动,顶点D在y轴的正半轴上运动(点A,D都不与原点重合),顶点B,C都在第一象限,且对角线AC,BD相交于点P,连接OP.