题目内容
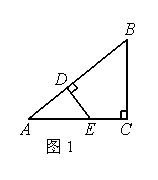
如图1,在△ABC,∠A=45°,延长CB至D,使得BD=BC.
(1)若∠ACB=90°,求证:BD=AC;
(2)如图2,分别过点D和点C作AB所在直线的垂线,垂足分别为E、F,求证:DE=CF;
(3)如图3,若将(1)中“∠ACB=90°”去掉,并在AB延长线上取点G,使得∠1=∠A”.试探究线段AC、DG的数量与位置关系.

(1)证明:∵∠A=45°,∠ACB=90°,∴∠ABC=∠A=45°,∴AC=BC,
∵BD=BC,∴BD=AC;
(2)证明:∵DE⊥AB,CF⊥AB,∴∠E=∠CFB=90°,
∵∠DBE=∠CBF,BD=BC,∴△DBE≌△CBF(AAS),∴DE=CF;
(3)解:DG=AC,DG⊥AC.
证明:过点C作CE∥DG交AB于点E,∴∠2=∠3,
∵∠1+∠2=180°,∠3+∠4=180°,∴∠1=∠4,∵∠1=∠A,∴∠4=∠A,∴AC=CE,
∵BD=BC,∠EBC=∠GBD,∠2=∠3,
∴△DBG≌△CBE(AAS),∴CE=DG,∴DG=AC.
∵∠A=45°,∴∠4+∠A=90°,∴∠ACE=90°,∴AC⊥CE,∴AC⊥DG.
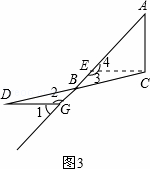 ∴DG=AC,DG⊥AC.
∴DG=AC,DG⊥AC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,再选取一个你喜欢的数代入求值。
,再选取一个你喜欢的数代入求值。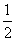 S△ABC;
S△ABC;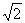 .上述结论始终正确的有( )
.上述结论始终正确的有( ) 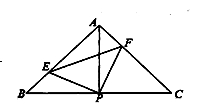
 ×(
×( )÷
)÷ .
. 
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6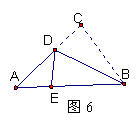
 ,
, ,
, ,
, ,
,
