题目内容
如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,结果精确到0.1)
≈2.45,结果精确到0.1)

考点:
解直角三角形的应用-方向角问题.
分析:
过点B作BD⊥CA交CA延长线于点D,根据题意可得∠ACB和∠ABC的度数,然后根据三角形外角定理求出∠DAB的度数,已知AB=12海里,可求出BD、AD的长度,在Rt△CBD中,解直角三角形求出CD的长度,继而可求出A、C之间的距离.
解答:
解:过点B作BD⊥CA交CA延长线于点D,
由题意得,∠ACB=60°﹣30°=30°,
∠ABC=75°﹣60°=15°,
∴∠DAB=∠DBA=45°,
在Rt△ABD中,AB=12,∠DAB=45°,
∴BD=AD=ABcos45°=6![]() ,
,
在Rt△CBD中,CD=![]() =6
=6![]() ,
,
∴AC=6![]() ﹣6
﹣6![]() ≈6.2(海里).
≈6.2(海里).
答:A、C两地之间的距离为6.2海里.

点评:
本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
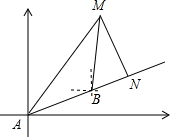 如图,在A黄岩岛东偏北30°方向上有一艘执行巡逻任务的中国海监船,同时在A黄岩岛东偏北60°方向有一艘中国渔船M正在海上作业.当我海监船向前行进到1800米的B处时,接到渔船发来的求救信号,信号显示,我渔船被菲律宾军舰“德尔毕拉尔”号扣留,即将沿MN方向将我渔船带回菲律宾.此时测得“德尔毕拉尔”号在我海监船的北偏东15°处,若MN⊥AB,我海监船继续向前行驶多少米可在N处拦截到“德尔毕拉尔”号?
如图,在A黄岩岛东偏北30°方向上有一艘执行巡逻任务的中国海监船,同时在A黄岩岛东偏北60°方向有一艘中国渔船M正在海上作业.当我海监船向前行进到1800米的B处时,接到渔船发来的求救信号,信号显示,我渔船被菲律宾军舰“德尔毕拉尔”号扣留,即将沿MN方向将我渔船带回菲律宾.此时测得“德尔毕拉尔”号在我海监船的北偏东15°处,若MN⊥AB,我海监船继续向前行驶多少米可在N处拦截到“德尔毕拉尔”号? (2013•烟台)如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于A北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据:
(2013•烟台)如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于A北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据: ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.45,结果精确到0.1)
≈2.45,结果精确到0.1)
 如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于A北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据:
如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于A北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据: ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.45,结果精确到0.1)
≈2.45,结果精确到0.1)