Question

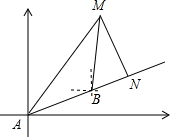如图，在A黄岩岛东偏北30°方向上有一艘执行巡逻任务的中国海监船，同时在A黄岩岛东偏北60°方向有一艘中国渔船M正在海上作业．当我海监船向前行进到1800米的B处时，接到渔船发来的求救信号，信号显示，我渔船被菲律宾军舰“德尔毕拉尔”号扣留，即将沿MN方向将我渔船带回菲律宾．此时测得“德尔毕拉尔”号在我海监船的北偏东15°处，若MN⊥AB，我海监船继续向前行驶多少米可在N处拦截到“德尔毕拉尔”号？
（参考数据：

3

=1.73，sin75°=0.97，cos75°=0.26，tan75°=3.73，结果精确到1m ）

Answer 1

分析：作BC⊥AM于点C，首先根据题意知∠MBN=75°，∠MAN=30°，从而得到∠AMB=45°，然后利用AB=1800米，求得BC后进一步求得BM，然后在直角三角形MNB中利用锐角三角函数求得BN的长即可．

解答：解：作BC⊥AM于点C．
∵由题意知∠MBN=75°，∠MAN=30°，
∴∠AMB=45°，
∵AB=1800米，
∴BC=

1

2

AB=

1

2

×1800=900米，
∴BM=

2

BC=900

2

米，
∴BN=BM•cos∠MBN=900

2

×0.26≈330米．

点评：本题考查了解直角三角形的应用，解题的关键是通过作辅助线构造直角三角形并解直角三角形．