��Ŀ����
����Ŀ����ͼ��P1��P2��P2��P1���Ҳࣩ��y= ![]() ��k��0���ڵ�һ�����ϵ����㣬��A1������Ϊ��2��0����
��k��0���ڵ�һ�����ϵ����㣬��A1������Ϊ��2��0����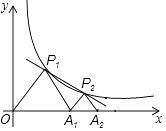
��1����գ�����P1�ĺ�����������ʱ����P1OA1�����������С�����䡢����
��2������P1OA1���P2A1A2��Ϊ�ȱ������Σ�
�����������Ľ���ʽ��
�������P2�����꣬������ͼ��ֱ��д�ڵ�һ�����ڣ���x����ʲô����ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y= ![]() �ĺ���ֵ��
�ĺ���ֵ��
���𰸡�
��1����С
��2���⣺����ͼ��ʾ����P1B��OA1�ڵ�B��
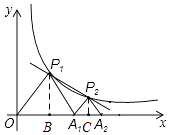
��A1��������2��0����
��OA1=2��
�ߡ�P1OA1�ǵȱ������Σ�
���P1OA1=60�㣬
�֡�P1B��OA1��
��OB=BA1=1��
��P1B= ![]() ��
��
��P1��������1�� ![]() ����
����
���뷴������������ʽ�ɵ�k= ![]() ��
��
�෴���������Ľ���ʽΪy= ![]() ��
��
����ͼ��ʾ����P2��P2C��A1A2�ڵ�C��
�ߡ�P2A1A2Ϊ�ȱ������Σ�
���P2A1A2=60�㣬
��A1C=x����P2C= ![]() x��
x��
���P2��������2+x�� ![]() x����
x����
���뷴������������ʽ�ɵã�2+x�� ![]() x=
x= ![]() ��
��
���x1= ![]() ��1��x2=��
��1��x2=�� ![]() ��1����ȥ����
��1����ȥ����
��OC=2+ ![]() ��1=
��1= ![]() +1��P2C=
+1��P2C= ![]() ��
�� ![]() ��1��=
��1��= ![]() ��
�� ![]() ��
��
���P2�������� ![]() +1��
+1�� ![]() ��
�� ![]() ����
����
�൱1��x�� ![]() +1ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y=
+1ʱ��������P1��P2��һ�κ����ĺ���ֵ���ڷ���������y= ![]() �ĺ���ֵ
�ĺ���ֵ
���������⣺��1������P1�ĺ�����������ʱ����P1��x��ľ����С����OA1�ij��Ȳ��䣬
�ʡ�P1OA1���������С��
���Դ��ǣ���С��

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д�����Ŀ��ijУΪӭ�������п����˽�ѧ�������������ѧУ��������˱�У���꼶50��ѧ����30���������Ĵ����������������õ������������£�
30������������Ƶ����Ƶ�ʷֲ���
�ɼ��� | Ƶ�� | Ƶ�� |
0��x��20 | 5 | 0.1 |
20��x��40 | 10 | a |
40��x��60 | b | 0.14 |
60��x��80 | m | c |
80��x��100 | 12 | n |
��������ͼ����Ϣ������������⣺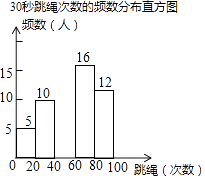
��1�����е�a= �� m=��
��2�����Ƶ���ֲ�ֱ��ͼ��������������ͼ�����ע��Ӧ�����ݣ�
��3������У���꼶����600��ѧ����������ơ�30���������Ĵ���60�����ϣ���60�Σ���ѧ���ж����ˣ�