题目内容
如图,直线y=kx(k>0)与双曲线y=交于A(x1,y1)、B(x2,y2)两点,则5x1y2﹣8x2y1的值为 12 .

考点:
反比例函数图象的对称性..
专题:
数形结合.
分析:
根据关于原点对称的点的坐标特点找出A、B两点坐标的关系,再根据反比例函数图象上点的坐标特点解答即可.
解答:
解:由题意知,直线y=kx(k>0)过原点和一、三象限,且与双曲线y=交于两点,则这两点关于原点对称,
∴x1=﹣x2,y1=﹣y2,
又∵点A点B在双曲线y=上,
∴x1×y1=4,x2×y2=4,
∴原式=﹣5x1y1+8x2y2=﹣20+32=12.
故答案为:12.
点评:
本题考查了反比例函数图象的对称性,难度一般,解答本题的关键是利用过原点的直线与双曲线的两个交点关于原点对称.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
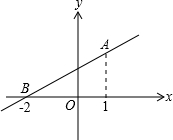 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为