题目内容
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【答案】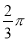
【解析】试题解析:依题意,n=60,r=2,
∴扇形的弧长= 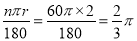 .
.
【题型】填空题
【结束】
13
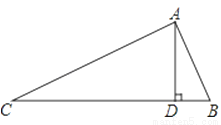
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
练习册系列答案
相关题目
题目内容
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【答案】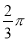
【解析】试题解析:依题意,n=60,r=2,
∴扇形的弧长= 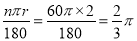 .
.
【题型】填空题
【结束】
13
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为________
