��Ŀ����
��ͼ����֪������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C������BC�������ߵĶԳ����ڵ�E��D�������ߵĶ��㣮
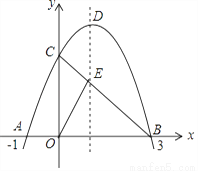
��1����������ߵĽ���ʽ��
��2��ֱ��д����C�͵�D�����ꣻ
��3������P�ڵ�һ�����ڵ��������ϣ���S��ABP=4S��COE �� ��P�����꣮
��1��y=-x2+2x+3��2��D��1��4����3��P��2��3�� �������������������1����A��B��������������ߵĽ���ʽ�У������������ϵ��b��c��ֵ�������ɵõ������ߵĶԳ��᷽�̣� ��2����x=0���ɵ�C�����꣬����������ʽ�䷽���������ߵĶ���C�����ꣻ ��3����P��x��y����x��0��y��0�������������г����̼������y������D�����꣮ ��1���ɵ�A����1��0���͵�B��3...
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


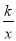 ��ͼ����P����1��2���������������ͼ��λ�ڣ� ��
��ͼ����P����1��2���������������ͼ��λ�ڣ� ��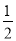 ��D����C��
��D����C��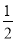 ��A�����B���C�Ķ���֮�ͣ�
��A�����B���C�Ķ���֮�ͣ�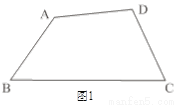
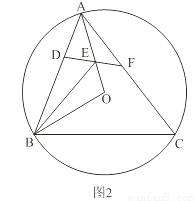
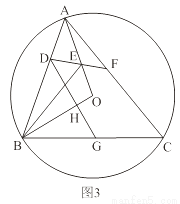
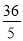 D.
D. 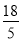
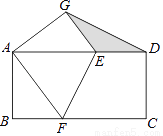
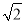 ��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
��CD�ǡ�ABC�������ָ��ߣ��ҡ�ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���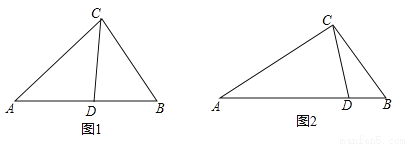
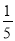 ����ô�ڴ���С����_____����
����ô�ڴ���С����_____����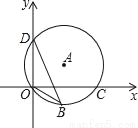
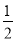 B.
B. 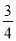 C.
C. 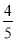 D.
D. 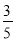
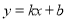 ��
��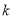 ��
�� 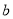 ������
Ϊ������ 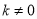 ����ͼ����ͼ��ʾ������ͼ����Ϣ����ù���
����ͼ����ͼ��ʾ������ͼ����Ϣ����ù���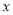 �ķ���
�ķ���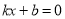 �Ľ�Ϊ__________��
�Ľ�Ϊ__________��