题目内容
 如图,∠AOM与∠BOM互余,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
如图,∠AOM与∠BOM互余,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.考点:余角和补角,角平分线的定义
专题:
分析:先由∠AOM与∠BOM互余,得出∠AOB=90°,再根据角平分线定义得出∠MOC=
∠AOC,∠NOC=
∠BOC,那么∠MON=∠MOC-∠NOC=
∠AOB=45°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠AOM与∠BOM互余,
∴∠AOM+∠BOM=90°,即∠AOB=90°.
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
∴∠MON=∠MOC-∠NOC=
∠AOC-
∠BOC=
(∠AOC-∠BOC)=
∠AOB=
×90°=45°.
∴∠AOM+∠BOM=90°,即∠AOB=90°.
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠MOC-∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查角平分线定义,互余的定义,得出∠MON=
∠AOB是解题的关键.
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x为任意数,则下列各式一定是正数的是( )
| A、|x| |
| B、x2 |
| C、x2+1 |
| D、-x |
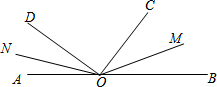 如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=50°,∠BOC=40°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )
如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=50°,∠BOC=40°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )| A、135° | B、140° |
| C、152° | D、45° |
计算(-2)2×(-
)2×(-1)2012得( )
| 1 |
| 2 |
| A、1 | B、-1 | C、±1 | D、2012 |
在平面直角坐标系中,点A(-2,-3)关于x轴对称点A′在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

 如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的三视图不变的情况下,该正方体最多还能放
如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的三视图不变的情况下,该正方体最多还能放 如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.
如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.