题目内容
已知抛物线 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线 经过点
经过点 ,方程
,方程 的两根为
的两根为 ,
, ,且
,且 。
。
(1)求抛物线 的顶点坐标.
的顶点坐标.
(2)已知实数 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
.
(3)若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线 ,设
,设 ,
, 是
是 上的两个不同点,且满足
上的两个不同点,且满足 :
: ,
, ,
, .
. 请你用含有
请你用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的最小值及
的最小值及 取最小值时一次函数
取最小值时一次函数 的函数解析式。
的函数解析式。
(参考公式:在平面直角坐标系中,若 ,
, ,则
,则 ,
, 两点间的距离为
两点间的距离为 )
)
 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线 经过点
经过点 ,方程
,方程 的两根为
的两根为 ,
, ,且
,且 。
。(1)求抛物线
 的顶点坐标.
的顶点坐标.(2)已知实数
 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
.(3)若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线
 ,设
,设 ,
, 是
是 上的两个不同点,且满足
上的两个不同点,且满足 :
: ,
, ,
, .
. 请你用含有
请你用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的最小值及
的最小值及 取最小值时一次函数
取最小值时一次函数 的函数解析式。
的函数解析式。(参考公式:在平面直角坐标系中,若
 ,
, ,则
,则 ,
, 两点间的距离为
两点间的距离为 )
)解:(1)∵抛物线 过点
过点
∴
∴
又∵方程 的两根为
的两根为 ,
,
∴ ,
,
 由
由 两边平方整理得:
两边平方整理得: 即
即
∴
又
∴
∴抛物线 的函数解析式为
的函数解析式为 
∴抛物线 的顶点坐标为
的顶点坐标为
(2)∵
∴ ,
, 
而 即
即
∴ ,
,
当且仅当 时,
时,
(3)由题意可求抛物线 的解析式为:
的解析式为:
∴ ,
, 过点
过点 、
、 作
作 轴的垂线,垂足分别为
轴的垂线,垂足分别为 、
、 ,
,
则


由

 得
得  即
即
∴
∴
∴

由(2)知:
∴
当且仅当 ,
, 取得最小值1此时
取得最小值1此时 的坐标为(1,1)
的坐标为(1,1)
∴一次函数 的解析式为
的解析式为
 过点
过点
∴

∴

又∵方程
 的两根为
的两根为 ,
,
∴
 ,
, 由
由 两边平方整理得:
两边平方整理得: 即
即
∴

又

∴

∴抛物线
 的函数解析式为
的函数解析式为 
∴抛物线
 的顶点坐标为
的顶点坐标为
(2)∵

∴
 ,
, 
而
 即
即
∴
 ,
,当且仅当
 时,
时,
(3)由题意可求抛物线
 的解析式为:
的解析式为:
∴
 ,
, 过点
过点 、
、 作
作 轴的垂线,垂足分别为
轴的垂线,垂足分别为 、
、 ,
,则



由


 得
得  即
即
∴

∴

∴


由(2)知:

∴

当且仅当
 ,
, 取得最小值1此时
取得最小值1此时 的坐标为(1,1)
的坐标为(1,1)∴一次函数
 的解析式为
的解析式为

练习册系列答案
相关题目
 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线
 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
. ,设
,设 用含有
用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的函数解析式。
的函数解析式。 ,则
,则 ,
, 两点间的距离为)
两点间的距离为)
 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+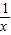 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+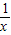 =2.
=2. ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+