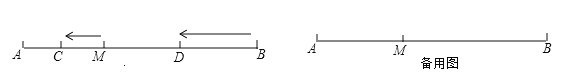题目内容
【题目】如图，已知数轴上有
、
、
三个点，它们表示的数分别是
，
，10，我们约定点与点之间的距离记为
，点与点之间的距离记为
．
（1）线段的长度为 ，线段的长度为 ；
（2）若点向左运动6个单位长度，则运动后的点表示的数为 ；若点向右运动6个单位长度，则运动后的点表示的数为 ；
（3）若点以每秒1个单位长度的速度向左运动，同时点和点分别以每秒3个单位长度和7个单位长度的速度向右运动，设运动时间为
秒．
①试用含的式子分别表示点、、运动秒后的位置所对应的数；
②试探索：
的值是否为定值？若是，请求出其定值；若不是，请说明理由．
【答案】（1）14，20；（2）
，
；（3）①
，
，
；②
的定值为6，详见解析．
【解析】
（1）画出数轴，根据数轴的性质求出线段
的长度和线段
的长度即可；
（2）若点
向左运动6个单位后对应的数为
，若点向右运动6个单位长度对应的数为
，分别列出对应的方程求解即可；
（3）分三种情况：①若点
向左运动
秒后对应点所对的数为
；②若点向右运动秒后对应点所对的数为
；③若点
向右运动秒后对应点所对的数为
，列出相应方程并求解即可求出A、B、C的值，从而求得AB、BC的值，即可得证的定值为6．
（1）如图所示：
、、三个点表示的数分别是
，
，10，
，
，
故答案为14，20；
（2）若点向左运动6个单位后对应的数为，依题意义得：
，
解得：
，
若点向右运动6个单位长度对应的数为，依题意义得：
，
解得：
，
故答案为：，；
（3）①若点向左运动秒后对应点所对的数为，
个单位长度
秒，
秒，
，
，
解得：
；
②若点向右运动秒后对应点所对的数为，
个单位长度秒，
秒，
，
，
解得：
；
③若点向右运动秒后对应点所对的数为，
个单位长度秒，
秒，
，
，
解得：
；
故答案为：，，；
②定值，理由如下：
，
，
，
即的定值为6．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
