题目内容
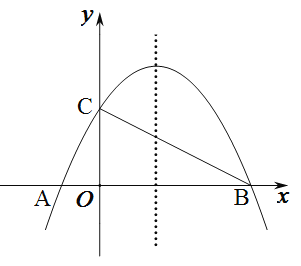
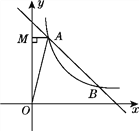
【题目】如图，是一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯，求两盏景观灯之间的水平距离（提示：请建立平面直角坐标系后，再作答）．
【答案】两盏景观灯之间的水平距离2
m．
【解析】
建立如图所示的平面直角坐标系，根据抛物线在坐标系的位置，可知抛物线的顶点坐标为（0，5），抛物线的左端点坐标为（﹣5，0），可设抛物线的顶点式求解析式，再根据两灯的纵坐标值，求横坐标，作差即可．
解：建立如图所示的平面直角坐标系，
由题意知点A（﹣5，0）、B（5，0）、C（0，5），
设抛物线解析式为y＝ax2+5，
将点A（﹣5，0）代入，得：25a+5＝0，
解得：a＝﹣
，
则抛物线解析式为y＝﹣x2+5，
当y＝4时，﹣x2+5＝4，
解得：x＝
，
则两盏景观灯之间的水平距离2m．
练习册系列答案
阅读快车系列答案
相关题目
【题目】运动员将小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间t（s）满足二次函数关系，t与h的几组对应值如下表所示．
t（s） | 0 | 0.5 | 1 | 1.5 | 2 | … |
h（m） | 0 | 8.75 | 15 | 18.75 | 20 | … |
（1）求h与t之间的函数关系式（不要求写t的取值范围）；
（2）求小球飞行3s时的高度；
（3）问：小球的飞行高度能否达到22m？请说明理由．
