题目内容
14.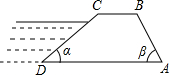 如图,拦水坝的横断面为四边形ABCD,且AD∥BC,上面CB=5m,迎水面的坡度为1:$\sqrt{3}$,背水面坡度为1:1,坝高为4m,求:
如图,拦水坝的横断面为四边形ABCD,且AD∥BC,上面CB=5m,迎水面的坡度为1:$\sqrt{3}$,背水面坡度为1:1,坝高为4m,求:(1)AD;
(2)CD;
(3)坡角α,β
分析 (1)过C点作CE⊥AD于点E,过B作BF⊥AD于点F,分别在△CDE和△ABF中求出DE、AF的长度,然后可求出AD;
(2)根据tana=$\frac{CE}{DE}$=$\frac{\sqrt{3}}{3}$得的α的度数,再利用三角函数求出CD的长度;
(3)根据tana=$\frac{CE}{DE}$=$\frac{\sqrt{3}}{3}$和tanβ=$\frac{BF}{FA}$=1:1可直接得出α,β的度数.
解答 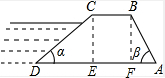 解:(1)过C点作CE⊥AD于点E,过B作BF⊥AD于点F,
解:(1)过C点作CE⊥AD于点E,过B作BF⊥AD于点F,
则四边形BCEF是矩形,有BC=EF=5,CE=BF=4,
∵tana=$\frac{CE}{DE}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴DE=4$\sqrt{3}$,
∵tanβ=$\frac{BF}{FA}$=1:1,
∴BF=AF=4,
∴AD=AF+EF+ED=4+5+4$\sqrt{3}$=(9+4$\sqrt{3}$)m;
(2)∵tana=$\frac{CE}{DE}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴α=30°,
∴DC=$\frac{4}{sin30°}$=8(m);
(3)由(2)可知α=30°,
∵tanβ=$\frac{BF}{FA}$=1:1,
∴β=45°.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形和矩形,利用锐角三角函数的概念和坡度的概念求解.

练习册系列答案
相关题目
19.使分式$\frac{2}{1-3x}$的值为正值的条件是( )
| A. | x<$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x<0 | D. | x>0 |
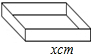 如图所示,设长方体底面是边长为xcm的正方形,高为20cm,
如图所示,设长方体底面是边长为xcm的正方形,高为20cm,