题目内容
如图,已知抛物线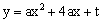 (a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(1)求此抛物线的对称轴及点A的坐标;
(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能
判断四边形ABCP是什么四边形吗?请证明你的结论;
(3)连结AC,BP,若AC⊥BP,试求此抛物线的解析式.
 |
解:(1)∵ ,
,
∴抛物线的对称轴是直线x=-2。
设点A的坐标为(x,0),
∵ ,∴x=-3。∴A的坐标(-3,0)。
,∴x=-3。∴A的坐标(-3,0)。
(2)四边形ABCP是平行四边形。证明如下:
∵抛物线的对称轴是直线x=-2,∴CP=2。
又∵AB=2,∴CP=AB。
又∵CP∥AB,∴四边形ABCP是平行四边形。
(3)∵AC⊥BP,∴平行四边形ABCP是菱形。
∴BC=AB=2。
又∵OB=1, ∴OC= 。∴C(0,
。∴C(0,  )。
)。
将B(-1,0), C(0,  )代入
)代入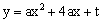 ,得:
,得:

 ,解得:
,解得: 。
。
∴此抛物线的解析式为 。
。


 名校课堂系列答案
名校课堂系列答案长为9,6,5,4的四根木条,选其中三根组成三角形,选法有( )
|
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
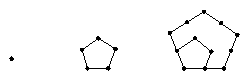
用棋子按下列方式摆图形,第一个图形有1枚棋子,第二个图形有5枚棋子,第三个图形有12枚棋子,…
依此规律,第7个图形比第6个图形多( )枚棋子
| |||||
 | |||||
 | |||||
|
|
|
|
A.20 B.19 C.18 D.17
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作
EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t(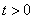 )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG, 得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
| |
 ,
, 之间的大小关系是 .
之间的大小关系是 .

