题目内容
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作
EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t(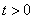 )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG, 得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
| |
解:(1)40;2 ………4分
(2) ………8分
………8分
(3)CM=CN时,
MC=MN时,
NM=NC时, ………12分
………12分

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
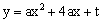 (a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).
(a>0)交x轴于A、B两点,交y轴于点C,点B的坐标为(-1,0).

 ,其中x是不等式
,其中x是不等式 的最大整数解.
的最大整数解.
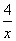 (x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OAC的面积为
(x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OAC的面积为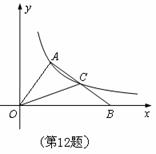
 B.
B. C.
C. D.
D.
 ∥
∥ 的条件有( ).
的条件有( ).