Question

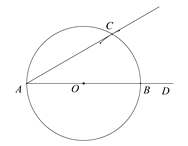
【题目】已知：如图，直线y＝﹣x+4与x轴相交于点A，与直线y＝x交于点P．

（1）求点P的坐标．

（2）动点F从原点O出发，以每秒1个单位的速度在线段OA上向点A作匀速运动，连接PF，设运动时间为t秒，△PFA的面积为S，求出S关于t的函数关系式．

（3）若点M是y轴上任意一点，点N是坐标平面内任意一点，若以O、M、N、P为顶点的四边形是菱形，请直接写出点N的坐标．

Answer 1

【答案】（1）P点坐标（2，2）；（2）S＝4﹣t（0≤t＜4）；（3）N点坐标为N1（2，2﹣4），N2（2，2+4），N3（﹣2，2），N4（2，）．

【解析】

（1）联立两直线的解析式求出x、y的值即可得出P点坐标；

（2）先求出A点坐标，再根据三角形的面积公式即可得出结论；

（3）分OP为菱形的边与对角线两种情况进行讨论．

解：（1）∵由已知，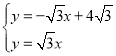

解得，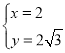

∴P点坐标（2，2）；

（2）∵直线y＝﹣x+4中，当y＝0时，x＝4，

∴OA＝4，

∴S＝（OA﹣t）×2＝（4﹣t）×2＝4﹣t（0≤t＜4）；

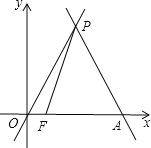
（3）如图，当OP为平行四边形的边时，

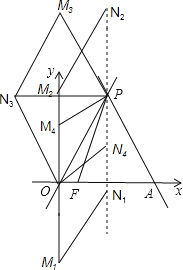
∵P（2，2），

∴OP＝＝4，

∴N1（2，2﹣4），N2（2，2+4），N3（﹣2，2）；

当OP为对角线时，设M（0，a），

则MP＝a，即22+（2﹣a）2＝a2，解得a＝，

∴N点的纵坐标＝2﹣＝，

∴N4（2，）．

综上所示，N点坐标为N1（2，2﹣4），N2（2，2+4），N3（﹣2，2），N4（2，）．