题目内容
如图，P是等边△ABC内一点，∠PBQ=60°，且BQ=BP，连接CQ．猜想AP与CQ之间的大小关系，并证明．
解：AP=CQ，
理由如下：∵△ABC是等边三角形，
∴AB=BC，∠ABC=60°．
∵∠PBQ=60°，
∴∠ABP=∠CBQ=60°-∠PBC．
在△ABP和△CBQ中，
，
∴△ABP≌△CBQ（SAS），
∴AP=CQ．
分析：AP=CQ，根据等边三角形的性质利用SAS判定△ABP≌△CBQ，从而得到AP=CQ．
点评：此题考查等边三角形的判定和性质、全等三角形的判定和性质及直角三角形的判定，难度中等．
理由如下：∵△ABC是等边三角形，
∴AB=BC，∠ABC=60°．
∵∠PBQ=60°，
∴∠ABP=∠CBQ=60°-∠PBC．
在△ABP和△CBQ中，
，∴△ABP≌△CBQ（SAS），
∴AP=CQ．
分析：AP=CQ，根据等边三角形的性质利用SAS判定△ABP≌△CBQ，从而得到AP=CQ．
点评：此题考查等边三角形的判定和性质、全等三角形的判定和性质及直角三角形的判定，难度中等．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC是等边三角形，AB=4cm，则BC边上的高AD等于
如图，△ABC是等边三角形，点D是线段BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交AB、AC于点F、G，连接BE．
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．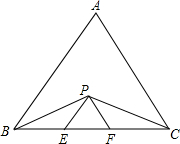
如图，△ABC是等边三角形，P为△ABC内任意一点，PE∥AB，PF∥AC．那么，△PEF是什么三角形？说明理由．