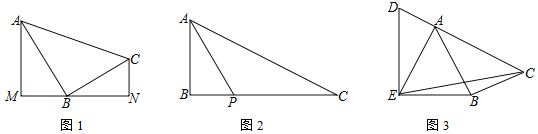
题目内容
【题目】在△ABC中,∠ABC=90°.
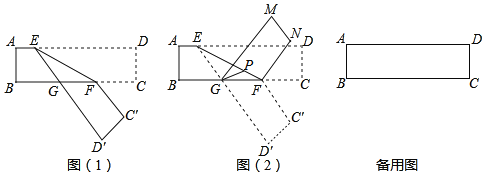
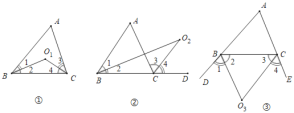
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)利用同角的余角相等判断出∠BAM=∠CBN,即可得出结论;
(2)如图,过点P作PF⊥AP交AC于F,先判断出△ABP∽△PQF,得出![]() ,再判断出△ABP∽△CQF,得出CQ=2a,进而建立方程用b表示出a,即可得出结论;
,再判断出△ABP∽△CQF,得出CQ=2a,进而建立方程用b表示出a,即可得出结论;
(3)先判断出![]() ,再同(2)的方法,即可得出结论.
,再同(2)的方法,即可得出结论.
(1)∵AM⊥MN,CN⊥MN,
∴∠AMB=∠BNC=90°,
∴∠BAM+∠ABM=90°,
∵∠ABC=90°,
∴∠ABM+∠CBN=90°,
∴∠BAM=∠CBN,
∵∠AMB=∠NBC,
∴△ABM∽△BCN;
(2)如图,过点P作PF⊥AP交AC于F,
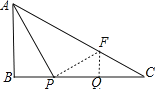
在Rt△AFP中,tan∠PAC=![]() ,
,
同(1)的方法得,△ABP∽△PQF,
∴![]() ,
,
设AB=![]() a,PQ=2a,BP=
a,PQ=2a,BP=![]() b,FQ=2b(a>0,b>0),
b,FQ=2b(a>0,b>0),
∵∠BAP=∠C,∠B=∠CQF=90°,
∴△ABP∽△CQF,
∴![]() ,∴CQ=
,∴CQ=![]() =2a,
=2a,
∵BC=BP+PQ+CQ=![]() b+2a+2a=4a+
b+2a+2a=4a+![]() b,
b,
∵∠BAP=∠C,∠B=∠B=90°,
∴△ABP∽△CBA,
∴![]() ,
,
∴BC=![]() ,
,
∴4a+![]() b=
b=![]() ,
,
∴a=![]() b,
b,
∴BC=4×![]() b+
b+![]() b=
b=![]() b,AB=
b,AB=![]() a=b,
a=b,
在Rt△ABC中,tanC=![]() ;
;
(3)在Rt△ABC中,sin∠BAC=![]() ,
,
如图,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,
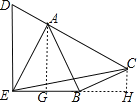
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
同(1)的方法得,△ABG∽△BCH,
∴![]() =
=![]() ,
,
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,
∴EG=BG=4m,
∴GH=BG+BH=4m+3n,
∴![]() ,
,
∴n=2m,
∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,
在Rt△CEH中,tan∠BEC=![]() .
.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
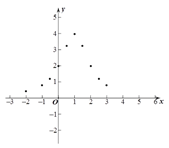
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .