题目内容
已知二次函数y=a(x-m)2-a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于点D.
①当△ABC的面积等于1时,求a的值;
②当△ABC的面积与△ABD的面积相等时,求m的值.
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于点D.
①当△ABC的面积等于1时,求a的值;
②当△ABC的面积与△ABD的面积相等时,求m的值.
考点:抛物线与x轴的交点
专题:
分析:(1)把(x-m)看作一个整体,令y=0,利用根的判别式进行判断即可;
(2)①令y=0,利用因式分解法解方程求出点A、B的坐标,然后求出AB,再把抛物线转化为顶点式形式求出顶点坐标,再利用三角形的面积公式列式进行计算即可得解;
②首先表示出D点坐标,进而利用三角形面积公式求出即可.
(2)①令y=0,利用因式分解法解方程求出点A、B的坐标,然后求出AB,再把抛物线转化为顶点式形式求出顶点坐标,再利用三角形的面积公式列式进行计算即可得解;
②首先表示出D点坐标,进而利用三角形面积公式求出即可.
解答:(1)证明:令y=0,a(x-m)2-a(x-m)=0,
△=(-a)2-4a×0=a2,
∵a≠0,
∴a2>0,
∴不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)解:①y=0,则a(x-m)2-a(x-m)=a(x-m)(x-m-1)=0,
解得:x1=m,x2=m+1,
∴AB=1,
y=a(x-m)2-a(x-m)=a(x-m-
)2-
a
△ABC的面积=
×1×|-
a|=1,
解得:a=±8.
②x=0时,y=a(0-m)2-a(0-m)=am2+am,
所以,点D的坐标为(0,am2+am),
△ABD的面积=
×1×|am2+am|,
∵△ABC的面积与△ABD的面积相等,
∴
×1×|am2+am|=
×1×|
|,
整理得,m2+m-
=0或m2+m+
=0,
解得:m=
或m=-
.
△=(-a)2-4a×0=a2,
∵a≠0,
∴a2>0,
∴不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)解:①y=0,则a(x-m)2-a(x-m)=a(x-m)(x-m-1)=0,
解得:x1=m,x2=m+1,
∴AB=1,
y=a(x-m)2-a(x-m)=a(x-m-
| 1 |
| 2 |
| 1 |
| 4 |
△ABC的面积=
| 1 |
| 2 |
| 1 |
| 4 |
解得:a=±8.
②x=0时,y=a(0-m)2-a(0-m)=am2+am,
所以,点D的坐标为(0,am2+am),
△ABD的面积=
| 1 |
| 2 |
∵△ABC的面积与△ABD的面积相等,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 4 |
整理得,m2+m-
| 1 |
| 4 |
| 1 |
| 4 |
解得:m=
-1±
| ||
| 2 |
| 1 |
| 2 |
点评:此题主要考查了二次函数与图象交点求法以及根的判别式、三角形的面积求法,把(x-m)看作一个整体求解更加简便.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
下列计算中,正确的( )
| A、(ab2)3=ab6 |
| B、(3xy)3=9x3y3 |
| C、(-2a2)2=-4a4 |
| D、(x-1)(x+1)=x2-1 |
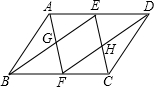 如图,在平行四边形ABCD中,如果E、F分别是边AD、BC的中点,BE交AF于G,DF交EC于H,那么四边形EGFH是平行四边形.请说明:
如图,在平行四边形ABCD中,如果E、F分别是边AD、BC的中点,BE交AF于G,DF交EC于H,那么四边形EGFH是平行四边形.请说明: 如图,BC平分∠ABE,DC∠平分ADE.求证:∠E+∠A=2∠C.
如图,BC平分∠ABE,DC∠平分ADE.求证:∠E+∠A=2∠C. 如图,计算∠A+∠B+∠C+∠D+∠E+∠F+∠AGF=
如图,计算∠A+∠B+∠C+∠D+∠E+∠F+∠AGF= 如图,在⊙O中,直径CE⊥弦AB于D,OD=3cm,弦AC=2
如图,在⊙O中,直径CE⊥弦AB于D,OD=3cm,弦AC=2