题目内容
 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N,给出以下三个结论:①MN∥AB;②
如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N,给出以下三个结论:①MN∥AB;② =
= +
+ ;③MN≤
;③MN≤ AB,其中正确结论的个数是
AB,其中正确结论的个数是
- A.0
- B.1
- C.2
- D.3
D
分析:(1)用平行线分线段成比例定理;
(2)根据相似三角形的性质,化简分式可得;
(3)要利用二次函数最值即可求解.
解答:(1)∵CD∥BE,
∴△CND∽△ENB,∴ ①
①
∵CE∥AD,
∴△AMD∽△EMC,∴ ②
②
∵等腰直角△ACD和△BCE,
∴CD=AD,BE=CE,
∴ ,
,
∴MN∥AB;
(2)∵CD∥BE,
∴△CND∽△ENB,
∴ ,
,
设 =k,
=k,
则CN=kNE,DN=kNB,
∵MN∥AB,
∴ =
= =
= ,
,
 =
= =
= ,
,
∴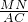 +
+ =1,
=1,
∴ =
= +
+ ;
;
(3)∵ =
= +
+ ,
,
∴MN= =
= ,
,
设AB=a(常数),AC=x,
则MN= x(a-x)=-
x(a-x)=- (x-
(x- a)2+
a)2+ a≤
a≤ a.
a.
点评:此题考查了三角形相似的判定与性质、平行线分线段成比例定理、比例变形及二次函数的应用.
分析:(1)用平行线分线段成比例定理;
(2)根据相似三角形的性质,化简分式可得;
(3)要利用二次函数最值即可求解.
解答:(1)∵CD∥BE,
∴△CND∽△ENB,∴
 ①
①∵CE∥AD,
∴△AMD∽△EMC,∴
 ②
②∵等腰直角△ACD和△BCE,
∴CD=AD,BE=CE,
∴
 ,
,∴MN∥AB;
(2)∵CD∥BE,
∴△CND∽△ENB,
∴
 ,
,设
 =k,
=k,则CN=kNE,DN=kNB,
∵MN∥AB,
∴
 =
= =
= ,
, =
= =
= ,
,∴
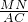 +
+ =1,
=1,∴
 =
= +
+ ;
;(3)∵
 =
= +
+ ,
,∴MN=
 =
= ,
,设AB=a(常数),AC=x,
则MN=
 x(a-x)=-
x(a-x)=- (x-
(x- a)2+
a)2+ a≤
a≤ a.
a.点评:此题考查了三角形相似的判定与性质、平行线分线段成比例定理、比例变形及二次函数的应用.

练习册系列答案
相关题目
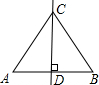 如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )
如图,已知CD是线段AB的垂直平分线,垂足为D,E是CD上一点.若∠A=60°,则下列结论中错误的是( )| A、AE=BE | B、AD=BD | C、AB=AC | D、ED=AD |
如图,已知C是线段AB的中点,则CD等于( )


| A、AD-BD | ||
B、
| ||
C、
| ||
D、AD-
|
 如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE.
如图,已知B是线段AE上一点,ABCD和BEFG都是正方形,连接AG、CE. (2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1
(2012•宿迁)如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1