题目内容
(1)解方程:x2-4x+1=0
(2)计算:-sin230°+(
-1)-1-2cos45°•tan45°
(3)计算:
+(
)-1-2sin60°+|tan60°-2|
(2)计算:-sin230°+(
| 2 |
(3)计算:
| 2 |
| 1 |
| 2 |
考点:二次根式的混合运算,负整数指数幂,解一元二次方程-配方法,特殊角的三角函数值
专题:计算题
分析:(1)利用配方法得到(x-2)2=3,然后利用直接开平方法解方程;
(2)根据负整数指数幂和特殊角的三角函数值得到原式=-(
)2+
-2×
×1,然后分母有理化后合并即可;
(3)根据负整数指数幂和特殊角的三角函数值得到原式=
+2-2×
+2-
,然后合并即可.
(2)根据负整数指数幂和特殊角的三角函数值得到原式=-(
| 1 |
| 2 |
| 1 | ||
|
| ||
| 2 |
(3)根据负整数指数幂和特殊角的三角函数值得到原式=
| 2 |
| ||
| 2 |
| 3 |
解答:解:(1)x2-4x+4=3,
(x-2)2=3,
x-2=±
,
所以x1=2+
,x2=2-
;
(2)原式=-(
)2+
-2×
×1
=-
+
+1-
=
;
(3)原式=
+2-2×
+2-
=4+
-2
.
(x-2)2=3,
x-2=±
| 3 |
所以x1=2+
| 3 |
| 3 |
(2)原式=-(
| 1 |
| 2 |
| 1 | ||
|
| ||
| 2 |
=-
| 1 |
| 4 |
| 2 |
| 2 |
=
| 3 |
| 4 |
(3)原式=
| 2 |
| ||
| 2 |
| 3 |
=4+
| 2 |
| 3 |
点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了负整数指数幂、特殊角的三角函数值和配方法解与一元二次方程.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图中的几何体是由6个大小相同的小正方体组成的,该几何体的俯视图为( )
如图中的几何体是由6个大小相同的小正方体组成的,该几何体的俯视图为( )A、 |
B、 |
C、 |
D、 |
下列计算或化简正确的是( )
A、2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
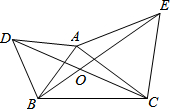 如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是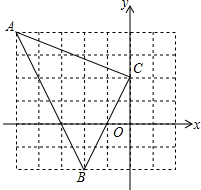 已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.
已知,如图点A(-5,4),B(-2,-2),C(0,2),求△ABC的周长.