Question

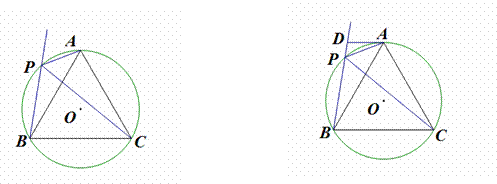
如图，PA为⊙O的切线，A为切点．过A作OP的垂线AB，垂足为点C，交⊙O于点B．延长BO与⊙O交于点D，与PA的延长线交于点E．

（1）求证：PB为⊙O的切线；（4分）

（2）若OC=1，AB=2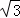，求图中阴影部分的面积S；（3分）

（3）若，求sinE的值．（3分）

  

Answer 1

 解：（1）证明：连接OA

∵PA为⊙O的切线，∴∠PAO=90°,  

∵OA＝OB，OP⊥AB于C，

∴BC＝CA，PB＝PA，∴△PBO≌△PAO

∴∠PBO＝∠PAO＝90°,∴PB为⊙O的切线.  

 (2) ∵OP⊥AB,∴BC=AC=，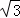

在Rt△OBC中，由tan∠BOC=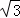知，∠BOC=60°，则∠BOA=120°，OB=2，

BP=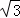OB=2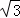

∴S=S_{四边形OBPA}﹣S_扇形OBA==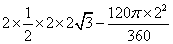

(3) 解法1：连接AD，∵BD是直径，∠BAD＝90°

由（1）知∠BCO＝90°,∴AD∥OP,

∴△ADE∽△POE,∴EA/EP＝AD/OP

由AD∥OC得AD＝2OC， 

∵tan∠ABE=1/2 ，  ∴OC/BC=1/2，

设OC＝t,则BC＝2t,AD=2t,

由△PBC∽△BOC，得PC＝2BC＝4t，OP＝5t

∴EA/EP=AD/OP=2/5，…………………（9分）

可设EA＝2m,EP=5m,则PA=3m

∵PA=PB∴PB=3m∴sinE=PB/EP=3/5.

解法2：连接AD，则∠BAD＝90°,

由（1）知∠BCO＝90°,∵由AD∥OC，∴AD＝2OC 

∵tan∠ABE=1/2,∴OC/BC=1/2,设OC＝t，BC＝2t，AB=4t

由△PBC∽△BOC，得PC＝2BC＝4t，∴PA＝PB＝2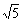t  

过A作AF⊥PB于F，则AF·PB=AB·PC∴AF=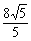t,

由勾股定理得PF＝t,

∴sinE=sin∠FAP=PF/PA=3/5.