题目内容
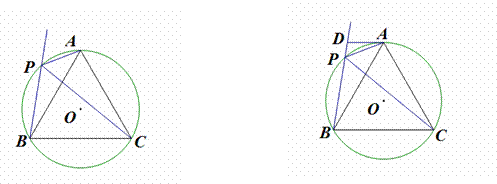
如图12-1,⊙O是等边三角形ABC的外接圆,点 P是 ⊙O 上一点,连结CP、AP,作射线BP.
(1)求证:PC平分∠APB;
(2)试猜想线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)如图12-2,过点A做⊙O的切线交射线BP于点D.若AD=2,PD=1,求⊙O的半径.
 |
(1)∵三角形ABC是等边三角形
∴∠BAC=∠ABC=∠ACB=60°………………………………………………1分
∵⊙O是等边三角形ABC的外接圆,点 P是 ⊙O 上一点,
∴∠BPC=∠BAC, ∠APC=∠ABC……………………………………………2分
∴∠BPC= ∠APC
∴PC平分∠APB………………………………………………………………3分
(2)PA+PB=PC, …………………………………………………………… ………4分
………4分
证明:在线段PC上截取PF=PB,连接BF,
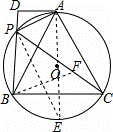 ∵PF=PB,∠BPC=60°,
∵PF=PB,∠BPC=60°,
∴△PBF是等边三角形,
∴PB=BF,∠BFP=60°,
∴∠BFC=180°﹣∠PFB=120°,
∵∠BPA=∠APC+∠BPC=120°,
∴∠BPA=∠BFC,……………………………………………………5分
在△BPA和△BFC中,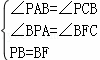 ,
,
∴△BPA≌△BFC(AAS),
∴PA=FC,AB=BC,
∴PA+PB=PF+FC=PC; ……………………………………………………6分
(其它证明方法按步骤酌情给分)
(3)作⊙O的直径AE,连接PE,
AE是⊙O的直径,AD是⊙O的切线,
∠DAE=∠APE=90°,
∴∠PAD+∠PAE=∠PAE+∠E=90°,
∴∠PAD=∠E,
∵∠PBA=∠E,∴∠PAD=∠PBA,
∵∠PAD=∠PBA,∠ADP=∠BDA,
∴△ADP∽△BDA,
∴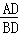 =
= =
= ,
,
∵AD=2,PD=1
∴BD=4,AB=2AP,
∴BP=BD﹣ DP=3,………………………………………………………………7分
DP=3,………………………………………………………………7分
∵∠APD=180°﹣∠BPA=60°,
∴∠APD=∠APC,
∵∠PAD=∠E,∠PCA=∠E,
∴∠PAD=∠PCA,
∴△ADP∽△CAP,………………………………………………… ……………8分
……………8分
∴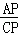 =
= ,
,
∴AP2=CP•PD,
∴AP2=(3+AP)•1,
解得:AP=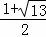 或AP=
或AP=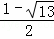 (舍去),
(舍去),
∴BC=AB=2AP=1+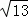 .………………………………………………………………9分
.………………………………………………………………9分
∴⊙O的半径为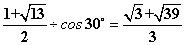 ……………………………………10分
……………………………………10分

下表是我市某一天在不同时段测得的气温情况:则这一天气温的极差是 ℃.
| 时间 | 0:00 | 4:00 | 8:00 | 12:00 | 16:00 | 20:00 |
| 气温 | 18℃ | 17℃ | 19℃ | 26℃ | 27℃ | 22℃ |
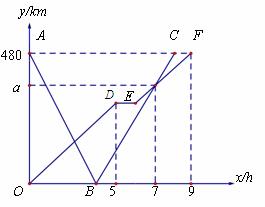

 ,其中
,其中 .
. = 时,代数式
= 时,代数式 与
与 的值相等。
的值相等。 B.
B. C.
C. D.
D.
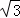 ,求图中阴影部分的面积S;(3分)
,求图中阴影部分的面积S;(3分) ,求sinE的值.(3分)
,求sinE的值.(3分)