题目内容
 如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA,OC分别落在x,y轴的正半轴上,连接AC,且AC=4
如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA,OC分别落在x,y轴的正半轴上,连接AC,且AC=4| 5 |
| OC |
| OA |
| 1 |
| 2 |
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后重叠部分的面积;
(3)求EF所在直线的函数解析式;
(4)若过一定点P的任意一条直线h总能够把矩形OABC的面积平均分为两部分,则顶点P的坐标为
考点:一次函数综合题
专题:
分析:(1)设OC=x,则OA=2x,在Rt△OAC中,根据勾股定理得到AC=
x,则
x=4
,解得x=4,得到A(8,0),C(0,4),然后利用待定系数法确定直线AC的解析式;
(2)设CE=t,根据折叠的性质得CE=AE=t,∠AEF=∠CEF,则OE=OA-AE=8-t,再根据勾股定理得到42+(8-t)2=t2,解得t=5,即CE=5,接着利用BC∥OA得到∠CFE=∠AEF,则∠CFE=∠CEF,所以CF=CE=5,然后根据三角形面积公式计算S△CEF;
(3)先确定E和F点的坐标,然后利用待定系数法确定直线EF的解析式;
(4)根据重心的性质得到经过矩形OABC的对角线的交点的直线总能够把矩形OABC的面积平均分为两部分,然后根据线段中点坐标公式求解.
| 5 |
| 5 |
| 5 |
(2)设CE=t,根据折叠的性质得CE=AE=t,∠AEF=∠CEF,则OE=OA-AE=8-t,再根据勾股定理得到42+(8-t)2=t2,解得t=5,即CE=5,接着利用BC∥OA得到∠CFE=∠AEF,则∠CFE=∠CEF,所以CF=CE=5,然后根据三角形面积公式计算S△CEF;
(3)先确定E和F点的坐标,然后利用待定系数法确定直线EF的解析式;
(4)根据重心的性质得到经过矩形OABC的对角线的交点的直线总能够把矩形OABC的面积平均分为两部分,然后根据线段中点坐标公式求解.
解答:解:(1)设OC=x,则OA=2x,
在Rt△OAC中,AC=
=
x,
∴
x=4
,解得x=4,
∴OC=4,OA=8,
∴A(8,0),C(0,4),
设直线AC的解析式为y=kx+b,
把A(8,0),C(0,4)代入得
,
解得
.
∴AC所在直线解析式为y=-
x+4;
(2)设CE=t,
∵纸片OABC折叠,使点A与点C重合(折痕为EF),
∴CE=AE=t,∠AEF=∠CEF,
∴OE=OA-AE=8-t,
在Rt△OCE中,∵OC2+OE2=CE2,
∴42+(8-t)2=t2,解得t=5,
即CE=5,
∵BC∥OA,
∴∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CF=CE=5,
∴S△CEF=
•5•4=10,
即折叠后重叠部分的面积为10;
(3)∵OE=OA-AE=3,
∴E点坐标为(3,0),
∵CF=5,
∴F点坐标为(5,4),
设直线EF的解析式为y=mx+n,
把E(3,0)、F(5,4)代入得
,
解得
,
∴直线EF的解析式为y=2x-6;
(4)经过矩形OABC的重心的直线总能够把矩形OABC的面积平均分为两部分,而矩形OABC的重心为对角线的交点,即线段AC的中点,线段AC的中点坐标为(4,2).
故答案为(4,2).
在Rt△OAC中,AC=
| OC2+OA2 |
| 5 |
∴
| 5 |
| 5 |
∴OC=4,OA=8,
∴A(8,0),C(0,4),
设直线AC的解析式为y=kx+b,
把A(8,0),C(0,4)代入得
|
解得
|
∴AC所在直线解析式为y=-
| 1 |
| 2 |
(2)设CE=t,
∵纸片OABC折叠,使点A与点C重合(折痕为EF),
∴CE=AE=t,∠AEF=∠CEF,
∴OE=OA-AE=8-t,
在Rt△OCE中,∵OC2+OE2=CE2,
∴42+(8-t)2=t2,解得t=5,
即CE=5,
∵BC∥OA,
∴∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CF=CE=5,
∴S△CEF=
| 1 |
| 2 |
即折叠后重叠部分的面积为10;
(3)∵OE=OA-AE=3,
∴E点坐标为(3,0),
∵CF=5,
∴F点坐标为(5,4),
设直线EF的解析式为y=mx+n,
把E(3,0)、F(5,4)代入得
|
解得
|
∴直线EF的解析式为y=2x-6;
(4)经过矩形OABC的重心的直线总能够把矩形OABC的面积平均分为两部分,而矩形OABC的重心为对角线的交点,即线段AC的中点,线段AC的中点坐标为(4,2).
故答案为(4,2).
点评:本题考查了一次函数的综合题:熟练掌握矩形的性质和折叠的性质;会利用待定系数法求函数解析式.

练习册系列答案
相关题目
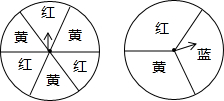 如图,用两个转盘进行“配绿色”游戏(黄色和蓝色配在一起为绿色),同时转动两个转盘,当转盘停止转动时,用两盘指针所指的颜色配色,求能配出绿色的概率(用树形图或列表法表示).
如图,用两个转盘进行“配绿色”游戏(黄色和蓝色配在一起为绿色),同时转动两个转盘,当转盘停止转动时,用两盘指针所指的颜色配色,求能配出绿色的概率(用树形图或列表法表示).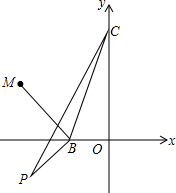 如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
如图,已知,B(-1,0)、C(0,3)、P(-2,-1),M(-2.5,1.5),若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标. 如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.