Question

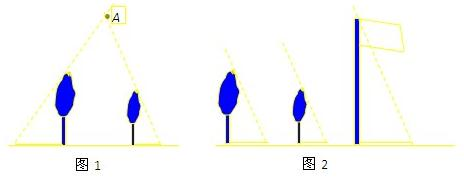
（1）如图1所示，两个直角三角形的直角顶点重合，已知∠AOD=120°，求∠BOC的度数；
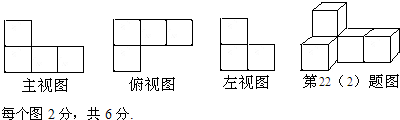
（2）请您画出图2的三视图；
（3）如图3，点O是MN上的一点，OA、OB、OC分别是从点O出发的三条射线，∠AOC是直角，OB平分∠MOC，若∠AOB=33°，求∠MOC的度数．

Answer 1

分析：（1）根据题意，将∠AOD分解为∠AOC+∠BOC+∠BOD，根据角的和差关系易得答案；
（2）主视图是从正面看所得到的图形，从左往右分别有2，1，1个小正方形；左视图是从左面看所得到的图形，从左往右分别有2，1，1个小正方形；俯视图是从上面看所得到的图形，从左往右分别有2，1个小正方形；
（3）先根据余角的定义求出∠BOC的度数，再根据角平分线的定义求出∠MOC的度数．

解答：（1）解：∵∠AOD=120°，∠COD=90°，
∴∠AOC=∠AOD-∠COD=30°，
∴∠BOC=90°-30°=60°；

（2）解：作图如下：


（3）解：∵∠AOC=90°，∠AOB=33°，
∴∠BOC=90°-33°=57°，
∵OB平分∠MOC，
∴∠MOC=2∠BOC=114°．

点评：（1）考查角的计算，注意结合图形，发现角与角之间的关系，利用公共角．
（2）主要考查了画三视图，关键是掌握三视图所看的位置．
（3）综合考查了余角的定义和角平分线的定义，角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．