题目内容
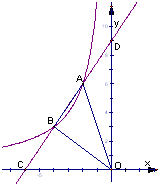
如图,直线AB与x轴、y轴分别交于点A、B,AB=5,cos∠OAB= ,直线
,直线 分别与直
分别与直 线AB、x轴、y轴交于点C、D、E.
线AB、x轴、y轴交于点C、D、E.
(1)求证:∠OED=∠OAB;
(2)直线DE上是否存在点P,使△PBE与△AOB相似,若存在,求点P的坐标;若不存在,请说明理由.
解:(1)在Rt△OAB中,∵AB=5,cos∠OAB= ,
,
∴OA=4,OB=3,
∴ =
= .
.
令x=0,则y=-1,∴OE=1.
令y=0,则 ,∴
,∴ ,∴OD=
,∴OD= .
.
∴ =
= .
.
∴ =
=
∵∠EOD=∠AOB=90°,
∴△EOD∽△AOB,
∴∠OED=∠OAB.

(2)分两种情况:
当∠EBP与∠AOB是对应角时,如图1,
则∠EBP=∠AOB=90°.
由(1)知,∠OAB=∠OED,OA=BE=4,
∴△BEP≌△AOB,
∴BP=OB=3,
将x=3代入 中,得
中,得 ,
,
∴点P(3,3).
当∠EBP与∠ABO是对应角时,如图2,则∠EBP=∠ABO.
∵∠OAB=∠OED,∴△EPB∽△AOB.
∵点P和点D都在直线CD上,
∴点C即为点P.
设直线AB解析式为y=kx+b.
将点A(4,0),点B(0,3)代入y=kx+b中,得 ,∴
,∴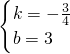 ,∴
,∴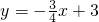 ,
,
∴ ,∴
,∴ ,∴点P(
,∴点P(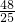 ,
, ).
).
分析:(1)利用题中已知条件求出直线AB的解析式,可知AB与CE是互相垂直的,然后证明∠OED=∠OAB;
(2)分两种情况讨论:①当∠EBP与∠AOB是对应角时;②当∠EBP与∠ABO是对应角时.对应不同情况解出点P的坐标.
点评:本题主要考查对一次函数的综合应用和相似三角形的应用.
 ,
,∴OA=4,OB=3,
∴
 =
= .
.令x=0,则y=-1,∴OE=1.
令y=0,则
 ,∴
,∴ ,∴OD=
,∴OD= .
.∴
 =
= .
.∴
 =
=
∵∠EOD=∠AOB=90°,
∴△EOD∽△AOB,
∴∠OED=∠OAB.

(2)分两种情况:
当∠EBP与∠AOB是对应角时,如图1,
则∠EBP=∠AOB=90°.
由(1)知,∠OAB=∠OED,OA=BE=4,
∴△BEP≌△AOB,
∴BP=OB=3,
将x=3代入
 中,得
中,得 ,
,∴点P(3,3).
当∠EBP与∠ABO是对应角时,如图2,则∠EBP=∠ABO.

∵∠OAB=∠OED,∴△EPB∽△AOB.
∵点P和点D都在直线CD上,
∴点C即为点P.
设直线AB解析式为y=kx+b.
将点A(4,0),点B(0,3)代入y=kx+b中,得
 ,∴
,∴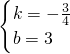 ,∴
,∴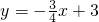 ,
,∴
 ,∴
,∴ ,∴点P(
,∴点P(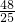 ,
, ).
).分析:(1)利用题中已知条件求出直线AB的解析式,可知AB与CE是互相垂直的,然后证明∠OED=∠OAB;
(2)分两种情况讨论:①当∠EBP与∠AOB是对应角时;②当∠EBP与∠ABO是对应角时.对应不同情况解出点P的坐标.
点评:本题主要考查对一次函数的综合应用和相似三角形的应用.

练习册系列答案
相关题目
 如图,直线AB与x轴交于点C,与反比例函数
如图,直线AB与x轴交于点C,与反比例函数 线AB、x轴、y轴交于点C、D、E.
线AB、x轴、y轴交于点C、D、E. 已知:如图,直线AB与x轴交于点A,与y轴交于点B.
已知:如图,直线AB与x轴交于点A,与y轴交于点B. 如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O逆时针旋转90°得到直线A1B1.
如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O逆时针旋转90°得到直线A1B1. 如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标
如图,直线AB与x轴、y轴分别交于点A、B,点A的坐标是(2,0),∠ABO=30°.在坐标平面内,是否存在点P(除点O外),使得△APB与△AOB全等.请写出所有符合条件的点P的坐标