题目内容
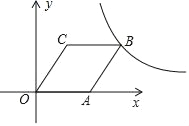
【题目】如图,点A是反比例函数y= ![]() (x>0)的图象上一点,OA与反比例函数y=
(x>0)的图象上一点,OA与反比例函数y= ![]() (x>0)的图象交于点C,点B在y轴的正半轴上,且AB=OA,若△ABC的面积为6,则k的值为________.
(x>0)的图象交于点C,点B在y轴的正半轴上,且AB=OA,若△ABC的面积为6,则k的值为________.

【答案】9
【解析】
过A作AH⊥BO于H,AE⊥x轴于E,过C作CD⊥x轴于D,由点A是反比例函数y=![]() (x>0)的图象上一点,得到S△AHO=S△AOE=
(x>0)的图象上一点,得到S△AHO=S△AOE=![]() k,根据等腰三角形的性质得到S△ABH=S△AOH=
k,根据等腰三角形的性质得到S△ABH=S△AOH=![]() k,求得S△AOB=k,由点C反比例函数y=
k,求得S△AOB=k,由点C反比例函数y=![]() (x>0)的图象上,得到S△COD=
(x>0)的图象上,得到S△COD=![]()
,根据相似三角形的性质得到![]() =
=![]() ,根据三角形的面积列方程即可得到结论.
,根据三角形的面积列方程即可得到结论.
解:过A作AH⊥BO于H,AE⊥x轴于E,过C作CD⊥x轴于D,
∵点A是反比例函数y=![]() (x>0)的图象上一点,
(x>0)的图象上一点,
∴S△AHO=S△AOE=![]() k,
k,
∵AB=AO,
∴BH=OH,
∴S△ABH=S△AOH=![]() k,
k,
∴S△AOB=k,
∵点C反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴S△COD=![]() ,
,
∵CD∥AE,
∴△COD∽△AOE,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵△ABC的面积为6,![]() =
=![]() ,
,
解得k=9,k=4(不合题意,舍去),
∴k=9.
故答案为:9.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④