Question

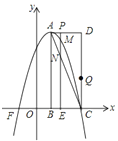
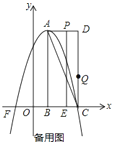
【题目】如图，在平面直角坐标系中，已知矩形的三个顶点，，，以为顶点的抛物线过点，动点从点出发，以每秒个单位的速度沿线段向点运动，运动时间为秒，过点作轴交抛物线于点，交于点．

直接写出点的坐标，并求出抛物线的解析式；

当为何值时，的面积最大？最大值为多少？

点从点出发，以每秒个单位的速度沿线段向点运动，当为何值时，在线段上存在点，使以，，，为顶点的四边形为菱形？

Answer 1

【答案】； 时，的最大值为．以，，，为顶点的四边形为菱形时，或．

【解析】

(1)A点的横坐标同B点，纵坐标同D点，然后设顶点式求解抛物线即可；

(2)求解直线的解析式为，设从而表示出M和N的坐标；将的面积拆分为和两部分进行计算即可；

(3)本问题分在上方和下方两种情况讨论，利用四边形是菱形的四边相等条件，将相关线段用t表示；当在上方时，运用三角形相似进行求解，当在下方时，运用勾股定理进行求解.

，

由题意知，可设抛物线解析式为

∵抛物线过点，

∴，

解得．

∴抛物线的解析式为，即；

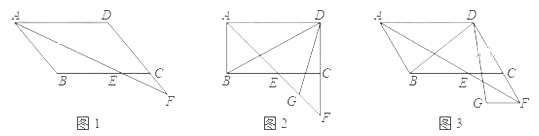
如图，

∵，，

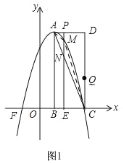
∴可求直线的解析式为．

∵点．

∴将代入中，解得点的纵坐标为，

∴把，代入抛物线的解析式中，可求点的纵坐标为，

∴，

又点到的距离为，到的距离为，

即

．

当时，的最大值为．

由题意和知，，，，，

，，可求，

当在上方时，如图，过点作，

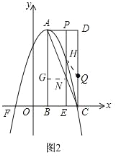
由四边形是菱形，可知：，

此时，，，

∴，

，

解得：，

当点在下方时，如图，

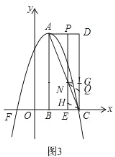
由四边形是菱形，可知：，

∴，，

在直角三角形中，，

∴，

解得或（舍去），

所以，以，，，为顶点的四边形为菱形时，或．